题目内容
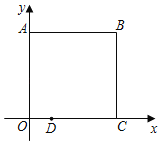
【题目】在平面直角坐标系中，A（0，4）、B（4，4）、C（4，0），D（1，0）．
（1）若抛物线经过A、B、D三点，求此抛物线的解析式；
（2）若（1）中的抛物线的顶点为E，连接EB，若P是EB上一动点，过P点作PM⊥AB，PN垂直于y轴，垂足分别是M、N．求矩形AMPN面积的最大值．
【答案】（1）y＝
x2
x+4；（2）最大值为
．
【解析】
（1）设抛物线的解析式为：y=ax2+bx+c，把A（0，4）、B（4，4）、D（1，0）代入y=ax2+bx+c列方程组即可得到结论；
（2）由（1）可知，抛物线的顶点坐标E（2，-），求得直线BE的解析式为y=
x-
，设P点的坐标为（m，m-），根据二次函数的性质即可得到结论．
解：（1）设抛物线的解析式为：y＝ax2+bx+c，
把A（0，4）、B（4，4）、D（1，0）代入y＝ax2+bx+c得，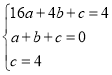
，
解得：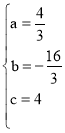
，
∴抛物线的解析式为：y＝x2x+4；；
（2）如图，
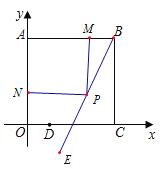
由（1）可知，抛物线的顶点坐标E（2，﹣），
设直线BE的解析式为：y=kx+b，把B为（4，4），E（2，﹣）代入得
，
∴
，
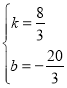∴直线BE的解析式为y＝x﹣，
∴设P点的坐标为（m，m﹣），
∴S矩形AMPN＝[4﹣（m﹣）]m﹣﹣m2+m＝﹣（m﹣2）2+，
∴当m＝2时，矩形AMPN面积的最大值为．
练习册系列答案
相关题目
【题目】二次函数y＝ax2+bx+c的自变量x与函数值y的对应值如图，下列说法错误的是：（ ）
x | … | ﹣6 | ﹣5 | ﹣4 | ﹣3 | ﹣2 | ﹣1 | … |
y | … | 10 | 4 | 0 | ﹣2 | ﹣2 | 0 | … |
A.抛物线开口向上
B.抛物线与y轴的交点是（0，4）
C.当x＜﹣2时，y随x的增大而减小
D.当x＞﹣2时，y随x的增大而增大
