题目内容
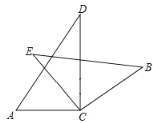
【题目】两块不同的三角板按如图所示摆放，两个直角顶点C重合，
，
。接着保持三角板ACD不动，将三角板CBE绕着点C旋转，但保证点E在直线AC的上方，若三角板CBE有一条边与斜边AD平行，则∠ACE＝__________.
【答案】30°或120°或165°
【解析】
根据题意，可分为三种情况进行①当AD∥BC时，②当AD∥CE时，当AD∥BE时，分别求出三种情况的角度，即可得到答案.
解：有三种情形：
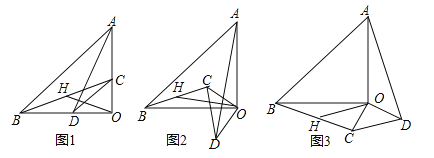
①如图1中，当AD∥BC时．
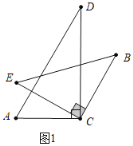
∵AD∥BC，
∴∠D=∠BCD=30°，
∵∠ACE+∠ECD=∠ECD+∠DCB=90°，
∴∠ACE=∠DCB=30°；
②如图2中，当AD∥CE时，∠DCE=∠D=30°，
可得∠ACE=90°+30°=120°．
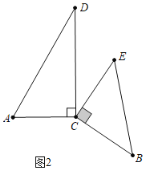
③如图3中，当AD∥BE时，延长BC交AD于M．
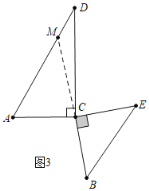
∵AD∥BE，
∴∠AMC=∠B=45°，
∴∠ACM=180°－60°－45°=75°，
∴∠ACE=75°+90°=165°，
综上所述，满足条件的∠ACE的度数为30°或120°或165°．
故答案是：30°或120°或165°．
练习册系列答案
相关题目
