Question

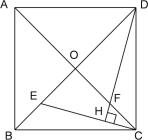
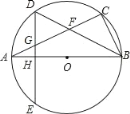
【题目】如图，点E是△ABC的内心，AE的延长线交BC于点F，交△ABC的外接圆⊙O于点D，连接BD，过点D作直线DM，使∠BDM＝∠DAC；

（1）求证：直线DM是⊙O的切线；

（2）若DF＝2，AF＝5，求BD长．

Answer 1

【答案】（1）见解析；（2）DB＝.

【解析】

（1）根据垂径定理的推论即可得到OD⊥BC，再根据∠BDM＝∠DBC，即可判定BC∥DM，进而得到OD⊥DM，据此可得直线DM是⊙O的切线；

（2）根据三角形内心的定义以及圆周角定理，得到∠BED＝∠EBD，即可得出DB＝DE，再判定△DBF∽△DAB，即可得到DB2＝DFDA，据此解答即可．

（1）如图所示，连接OD，

∵点E是△ABC的内心，

∴∠BAD＝∠CAD，

∴，

∴OD⊥BC，

又∵∠BDM＝∠DAC，∠DAC＝∠DBC，

∴∠BDM＝∠DBC，

∴BC∥DM，

∴OD⊥DM，

又∵OD为⊙O半径，

∴直线DM是⊙O的切线；

（2），

∴∠DBF＝∠DAB，

又∵∠BDF＝∠ADB（公共角），

∴△DBF∽△DAB，

∴=，即DB2＝DFDA，

∵DF＝2，AF＝5∴DA＝DF+AF＝7

∴DB2＝DFDA＝14

∴DB＝．