题目内容
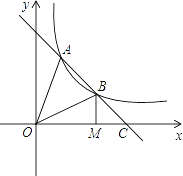
【题目】如图,已知二次函数![]() .
.
(1)求证:它的图象与x轴必有两个不同的交点;
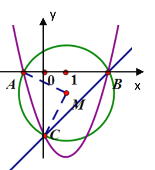
(2)这条抛物线与x轴交于两点A(x1,0),B(x2,O)(x1<x2),与y轴交于点C,且AB=4,⊙M过A,B,C三点,求扇形MAC的面积S;
(3)在(2)的条件下,抛物线上是否存在点P,PD⊥x轴于D,使△PBD被直线BC分成面积比为1:2的两部分?若存在,请求出P点的坐标;若不存在,请说明理由.
【答案】(1)见解析;(2)![]() ;(3)(3)P为(2,-3)或(
;(3)(3)P为(2,-3)或(![]() ,
,![]() ).
).
【解析】
(1)计算判别式△=(m+3)2>0,即可判断抛物线与x轴有两个不同的交点.
(2)根据抛物线的解析式,可表示出A、B的坐标,根据AB=4,可求出m的值,从而确定该抛物线的解析式,即可得到A、B、C的坐标;根据B、C的坐标,可得到∠OBC=45°,根据圆周角定理知∠AMC=90°,即△AMC是等腰直角三角形,AC的长易求得,即可得到半径AM、MC的长,利用扇形的面积公式,即可求得扇形AMC的面积.
(3)设PD与BC的交点为E,此题可分成两种情况考虑:
①当△BPE的面积是△BDE的2倍时,由于△BDE和△BPD同高不等底,那么它们的面积比等于底边的比,即DE=![]() PD,可设出P点的坐标,那么E点的纵坐标是P点纵坐标的
PD,可设出P点的坐标,那么E点的纵坐标是P点纵坐标的![]() ,BD的长为B、P横坐标差的绝对值,由于∠OBC=45°,那么BD=DE,可以此作为等量关系求出P点的坐标;
,BD的长为B、P横坐标差的绝对值,由于∠OBC=45°,那么BD=DE,可以此作为等量关系求出P点的坐标;
②当△BDE的面积是△BPE的2倍时,方法同①.
(1)∵△=(m+3)2>0,
∴与x轴有两个不同的交点.
(2)∵![]()
∴![]()
∴m=1
∴![]()
∴A(-1,0),B(3,0),C(0.3)
∴M(1,1)
∴R=![]() ,n=90°
,n=90°
∴![]()
(3)设P为(t, ![]() ),则D为(t,0)
),则D为(t,0)
因为![]() ,所以DP与BC的交点Q为(t,t-3)
,所以DP与BC的交点Q为(t,t-3)
当△PBD被BC分为1:2两部分时,![]()
即![]()
解得t1=2,t2=3(舍),t3=3(舍),t4=![]()
综上,P为(2,-3)或(![]() ,
,![]() )
)

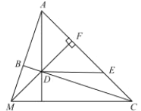
【题目】如图 1,在等腰△ABC 中,AB=AC,点 D,E 分别为 BC,AB 的中点,连接 AD.在线段 AD 上任取一点 P,连接 PB,PE.若 BC=4,AD=6,设 PD=x(当点 P 与点 D 重合时,x 的值为 0),PB+PE=y.
小明根据学习函数的经验,对函数y 随自变量x 的变化而变化的规律进行了探究. 下面是小明的探究过程,请补充完整:
(1)通过取点、画图、计算,得到了 x 与 y 的几组值,如下表:
x | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
y | 5.2 | 4.2 | 4.6 | 5.9 | 7.6 | 9.5 |
说明:补全表格时,相关数值保留一位小数.(参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732,
≈1.732,![]() ≈2.236)
≈2.236)
(2)建立平面直角坐标系(图 2),描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;
(3)求函数 y 的最小值(保留一位小数),此时点 P 在图 1 中的什么位置.