题目内容
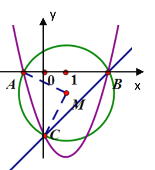
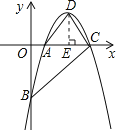
【题目】抛物线y=-x2+5x+n经过点A(1,0),与x轴交于点C,与y轴交于点B,顶点为D.
(1)求n的值和D点坐标;
(2)求四边形ABCD的面积.
【答案】(1)n=-4, D(![]() ,
,![]() );(2)S四边形ABCD =
);(2)S四边形ABCD =![]()
【解析】
(1)先把(1,0)代入函数解析式,可得关于n的一元一次方程组,解即可求n,然后代入解析式,把解析式化为顶点式,或者利用顶点坐标公式,就可以得出顶点D的坐标;
(2)先过D作DE⊥x轴于E,利用顶点的计算公式易求顶点D的坐标,通过观察可知S四边形ABCD=S△ACD+S△ABC,进而可求四边形ABCD的面积.
解:(1)∵抛物线y=-x2+5x+n经过点A(1,0),
∴0=-1+5+n,
∴n=-4,
∴抛物线的解析式为:y=-x2+5x-4=-(x-![]() )2+
)2+![]()
∴顶点D的坐标为(![]() ,
,![]() )
)
(2)过D作DE⊥x轴于E,
∵此函数的对称轴是x=2.5,顶点D的坐标为(![]() ,
,![]() ),并知C点的坐标是(4,0),B点坐标为:(0,-4),
),并知C点的坐标是(4,0),B点坐标为:(0,-4),
∴S四边形ABCD=S△ACD+S△ABC=![]() ACDE+
ACDE+![]() ACOB=
ACOB=![]() ×3×
×3×![]() +
+![]() ×3×4=
×3×4=![]() .
.

练习册系列答案
 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目