Question

【题目】如图，正方形ABCE的边长为1，点M、N分别在BC、CD上，且△CMN的周长为2，则△MAN的面积的最小值为（ ）

A.
B.
C.
D.

Answer 1

【答案】A
【解析】解：延长CB至L，使BL=DN， 则Rt△ABL≌Rt△AND，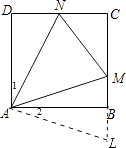

故AL=AN，
∴△AMN≌△AML，
∴∠MAN=∠MAL=45°，
设CM=x，CN=y，MN=z x2+y2=z2 ，
∵x+y+z=2， 则x=2-y-z
∴（2-y-z）2+y2=z2 ，
整理得2y2+（2z-4）y+（4-4z）=0，
∴△=4（z-2）2-32（1-z）≥0，
即（z+2+2 ）（z+2-2 ）≥0，
又∵z＞0，
∴z≥2 -2，
当且仅当x=y=2- 时等号成立 此时S△AMN=S△AML= MLAB= z
因此，当z=2 -2，x=y=2- 时，S△AMN取到最小值为 -1．
所以答案是：A．
【考点精析】利用二次函数的最值对题目进行判断即可得到答案，需要熟知如果自变量的取值范围是全体实数，那么函数在顶点处取得最大值（或最小值），即当x=-b/2a时，y最值=(4ac-b2)/4a．