题目内容
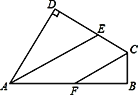
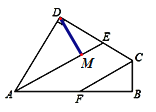
【题目】已知:如图所示,四边形ABCD中,∠B=∠D=90°,AE平分∠DAB,AE//CF.
(1)说明:CF平分∠BCD;
(2)作△ADE的高DM,若AD=8,DE=6,AE=10,求DM的长。
【答案】(1)略 (2)4.8
【解析】
(1)由AE∥CF,AE平分∠DAB,可证∠DAE=∠CFB,再由余角的性质可证∠DEA=∠BCF,进而可得∠DCF=∠BCF;
(2)右侧面积法求解即可.
(1)∵AE∥CF,
∴∠DEA=∠DCF,∠CFB=∠EAB,
∵AE平分∠DAB,
∴∠DAE=∠BAE,
∴∠DAE=∠CFB,
又∵∠BCF+∠BFC=90°,∠DEA+∠DAE=90°,
∴∠DEA=∠BCF,
∴∠DEA=∠DCF=∠BCF.
∴∠DCF=∠BCF,
∴CF平分∠BCD.
(2)如图,
∵![]() ,
,
∴10DM=8×6,
∴DM=4.8.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目