Question

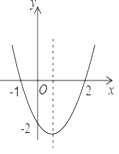
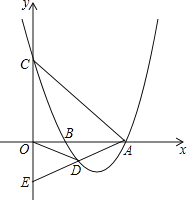
【题目】如图，抛物线y=mx2-16mx+48m(m＞0)与x轴交于A、B两点(点B在点A左侧)，与y轴交于点C，点D是抛物线上的一个动点，且位于第四象限，连接OD、BD、AC、AD，延长AD交y轴于点E.

(1)若△OAC为等腰直角三角形，求m的值.

(2)若对任意m＞0，C、E两点总关于原点对称，求点D的坐标(用含m的式子表示).

(3)当点D运动到某一位置时，恰好使得∠ODB=∠OAD，且点D为线段AE的中点，此时对于该抛物线上任意一点P(x0，y0)总有n≥－4my02－12y0-50成立，求实数n的最小值.

Answer 1

【答案】(1)m=；(2)点D的坐标为(8，-16m)；(3)实数n的最小值为

【解析】

（1）根据y=mx2-16mx+48m=m(x-4)(x-12)，可得A（12，0），C（0，48m），再根据OA＝OC，即可得到12＝48m，进而得出m的值；
（2）根据C、E两点总关于原点对称，得到E（0，48m），根据E（0，48m），A（12，0）可得直线AE的解析式，最后解方程组即可得到直线AE与抛物线的交点D的坐标；
（3）根据△ODB∽△OAD，可得OD＝4，进而得到D（6，2），代入抛物线y＝mx216mx＋48m，求出m可得抛物线解析式，再根据点P（x0，y0）为抛物线上任意一点，即可得出y0≥，令t＝-4my02-12y0-50，求出t最大值＝2（）2＋4＝，即可得实数n的最小值为．

解：(1)令y=mx2-16mx+48m=m(x-4)(x-12)=0，

则x1=12，x2=4，

∴A(12，0)，即OA=12，

又∵C(0，48m)，

∴当△OAC为等腰直角三角形时，OA=OC，即12=48m，

∴m=；.

(2)由(1)可知点C(0，48m)，

∵对任意m＞0，C、E两点总关于原点对称，

∴必有E(0，-48m)，

设直线AE的解析式为y=kx+b（k≠0），

将E(0，-48m)，A(12，0)代入，可得 ，解得，

∴直线AE的解析式为y=4mx-48m，

∵点D为直线AE与抛物线的交点，

∴解方程组，得或(舍去)，

∴点D的坐标为(8，-16m)；

(3)当∠ODB=∠OAD，∠DOB=∠AOD时，△ODB∽△OAD，

∴，

∴OD2=OA×OB=12×4=48，

∴OD=4，

又∵点D为线段AE的中点，

∴AE=2OD=8，

又∵OA=12，

∴OE= =4，

∴D(6，-2)，

把D(6，-2)代入抛物线y=mx2-16mx+48m，可得-2=36m-96m+48m，

解得：m=，

∴抛物线的解析式为y=(x-4)(x-12)，即y=(x-8)2-，

∵点P(x0，y0)为抛物线上任意一点，

∴y0≥-，

令t=-4my02-12y0-50=-2y02-12y0-50=-2(y0+3)2+4，

则当y0≥-时，t最大值=-2(-+3)2+4=，

若要使n≥-4my02-12y0-50成立，则n≥，

∴n≥，

∴实数n的最小值为.