Question

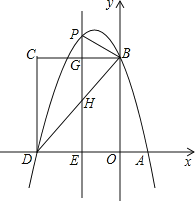
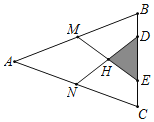
【题目】在△ABC中，AB＝AC＝13cm，BC＝10cm，M、N分别是AB、AC的中点，D、E在BC上，且DE＝5cm，连结DN、ME交于H，则△HDE的面积为_____．

Answer 1

【答案】cm2．

【解析】

根据题意，易得MN＝DE，从而证得△DEH≌△NMH，再进一步求△DHE的高，则阴影部分的面积可求．

解：连接MN，作AK⊥BC于K．

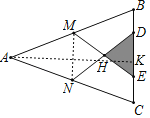
∵AB＝AC，

∴BK＝CK＝BC＝×10＝5cm，

在Rt△ABK中，AK＝

∵M、N分别是AB，AC的中点，

∴MN是中位线且平分三角形的高，

∴MN＝BC＝DE，MN∥BC，∠MNH＝∠HDE，∠NMH＝∠HED，

∴△DEH≌△GFH（ASA），

∴MH＝HE，NH＝DH，

∴H也是DN，EM的中点，

∴△HDE的高是

∴S△HDE＝

故答案为：