题目内容
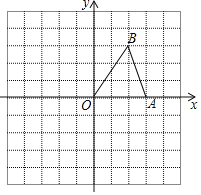
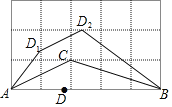
【题目】如图,在正方形网格中,△ABC的每一个顶点都在格点上,AB=5,点D是AB边上的动点(点D不与点A,B重合),将线段AD沿直线AC翻折后得到对应线段AD1,将线段BD沿直线BC翻折后得到对应线段BD2,连接D1D2,则四边形D1ABD2的面积的最小值是 ____.
【答案】5![]()
【解析】
延长AC使CE=AC,先证明△BCE是等腰直角三角形,再根据折叠的性质解得S四边形ADCD1+S四边形BDCD2=5,再根据S四边形D1ABD2=S四边形ADCD1+S四边形BDCD2+S△D1CD2,可得要四边形D1ABD2的面积最小,则△D1CD2的面积最小,即:CD最小,此时,CD⊥AB,此时CD最小=1,根据三角形面积公式即可求出四边形D1ABD2的面积的最小值.
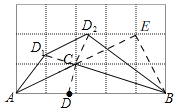
如图,
延长AC使CE=AC,
∵点A,C是格点,
∴点E必是格点,
∵CE2=12+22=5,BE2=12+22=5,BC2=12+32=10,
∴CE2+BE2=BC2,CE=BE,
∴△BCE是等腰直角三角形,
∴∠BCE=45°,
∴∠ACB=135°,
由折叠知,∠DCD1=2∠ACD,∠DCD2=2∠BCD,
∴∠DCD1+∠DCD2=2(∠ACD+∠BCD)=2∠ACB=270°,
∴∠D1CD2=360°﹣(∠DCD1+DCD2)=90°,
由折叠知,CD=CD1=CD2,
∴△D1CD2是等腰直角三角形,
由折叠知,△ACD≌△ACD1,△BCD≌△BCD2,
∴S△ACD=S△ACD1,S△BCD=S△BCD2,
∴S四边形ADCD1=2S△ACD,S四边形BDCD2=2S△BCD,
∴S四边形ADCD1+S四边形BDCD2
=2S△ACD+2S△BCD
=2(S△ACD+S△BCD)
=2S△ABC
=5,
∴S四边形D1ABD2=S四边形ADCD1+S四边形BDCD2+S△D1CD2,
∴要四边形D1ABD2的面积最小,则△D1CD2的面积最小,
即:CD最小,此时,CD⊥AB,
此时CD最小=1,
∴S△D1CD2最小=![]() CD1CD2=
CD1CD2=![]() CD2=
CD2=![]() ,
,
即:四边形D1ABD2的面积最小为5+![]() =5.5,
=5.5,
故答案为5.5.

 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案