题目内容
【题目】如图,有一直角三角形纸片![]() ,边
,边![]() ,
,![]() ,
,![]() ,将该直角三角形纸片沿
,将该直角三角形纸片沿![]() 折叠,使点
折叠,使点![]() 与点
与点![]() 重合,则四边形
重合,则四边形![]() 的周长为______.
的周长为______.
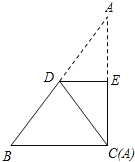
【答案】18.
【解析】
先由折叠的性质得AE=CE,AD=CD,∠DCE=∠A,进而得出,∠B=∠BCD,求得BD=CD=AD=![]() AB=5,DE为△ABC的中位线,得到DE的长,再在Rt△ABC中,由勾股定理得到AC=8,即可得四边形DBCE的周长.
AB=5,DE为△ABC的中位线,得到DE的长,再在Rt△ABC中,由勾股定理得到AC=8,即可得四边形DBCE的周长.
∵沿DE折叠,使点A与点C重合,
∴AE=CE,AD=CD,∠DCE=∠A,
∴∠BCD=90°-∠DCE,
又∵∠B=90°-∠A,
∴∠B=∠BCD,
∴BD=CD=AD=![]() AB=5,
AB=5,
∴DE为△ABC的中位线,
∴DE=![]() BC=3,
BC=3,
∵BC=6,AB=10,∠ACB=90°,
∴AC=![]() ,
,
∴四边形DBCE的周长为:BD+DE+CE+BC=5+3+4+6=18.
故答案为:18.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目