题目内容
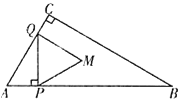
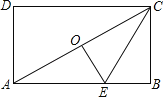
【题目】如图，矩形ABCD中，过对角线AC的中点O作OE⊥AC交AB于点E，连接CE，若BC＝
，OE＝BE，则CE的长为_____．
【答案】2
【解析】
由角平分线判定定理得到EC平分∠BCO，利用线段的垂直平分线的性质及等腰三角形的性质得到∠EAO=∠OCE=∠ECB，再由三角形外角的性质及三角形内角和定理得出∠ECB=30°，再根据含30°角的直角三角形的性质得出CE的长即可．
∵四边形ABCD是矩形，OE⊥AC，∴∠EOC=∠B=90°．
∵OE=BE，∴∠OCE=∠BCE．
∵OE⊥AC，AO=OC，∴EC=AE，∴∠EAO=∠ECO，∴∠EAO=∠OCE=∠ECB，∴∠CEB=∠EAO+∠ECO=2∠ECB．
∵∠ECB+∠CEB=90°，∴∠ECB=30°．
∵BC=
，∴BE=1，EC=2．
故答案为2．
练习册系列答案
相关题目
