题目内容
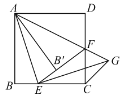
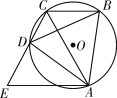
【题目】如图,四边形ABCD内接于⊙O,AC与BD为对角线,∠BCA=∠BAD,过点A作AE∥BC交CD的延长线于点E.
(1)求证:EC=AC;
(2)若cos∠ADB=![]() ,BC=10,求DE的长.
,BC=10,求DE的长.
【答案】(1)证明见解析;(2)DE=8.
【解析】
(1)根据平行线的性质可得∠ACB=∠EAC,从而得到∠EAD=∠CAB,由等量代换得到∠ADE=∠ABC,结合三角形的内角和得到∠E=∠ACB=∠EAC即可证明EC=AC.
(2)设AE交⊙O于M,连接DM,作MH⊥DE于H.通过圆的性质以及角的等量代换得到MD=ME=BC=10,解直角三角形求出EH即可解决问题.
(1)证明:∵BC∥AE,
∴∠ACB=∠EAC,
∵∠ACB=∠BAD,
∴∠EAC=∠BAD,
∴∠EAD=∠CAB.
∵∠ADE+∠ADC=180°,∠ADC+∠ABC=180°,
∴∠ADE=∠ABC,
∵∠EAD+∠ADE+∠E=180°,∠BAC+∠ABC+∠ACB=180°,
∴∠E=∠ACB=∠EAC,
∴EC=AC.
(2)解:设AE交⊙O于点M,连接DM,过点M作MH⊥DE于点H,
∵∠EAD=∠CAB,
∴![]() ,
,
∴DM=BC=10,
∵∠MDE+∠MDC=180°,∠MDC+∠MAC=180°,
∴∠MDE=∠CAM,
∵∠E=∠CAE,
∴∠E=∠MDE,
∴MD=ME=10,
∵MH⊥DE,
∴EH=DH,
∵∠ADB=∠ACB=∠BAD=∠E,
∴cos∠ADB=cos∠E=![]() ,
,
∴EH=4,
∴DE=2EH=8.
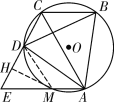

练习册系列答案
相关题目