题目内容
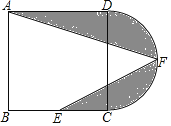
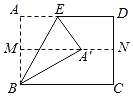
【题目】如图，对折矩形纸片ABCD使AD与BC重合，得到折痕MN，再把纸片展平．E是AD上一点，将△ABE沿BE折叠，使点A的对应点A′落在MN上．若CD＝5，则BE的长是_____．
【答案】
【解析】
在Rt△A'BM中，利用轴对称的性质与锐角三角函数求出∠BA′M=30°，再证明∠ABE=30°即可解决问题．
解：∵将矩形纸片ABCD对折一次，使边AD与BC重合，得到折痕MN，
∴AB=2BM，∠A′MB=90°，MN∥BC．
∵将△ABE沿BE折叠，使点A的对应点A′落在MN上．
∴A′B=AB=2BM．
在Rt△A′MB中，∵∠A′MB=90°，
∴sin∠MA′B= 
＝
，
∴∠MA′B=30°，
∵MN∥BC，
∴∠CBA′=∠MA′B=30°，
∵∠ABC=90°， ∴∠ABA′=60°，
∴∠ABE=∠EBA′=30°，
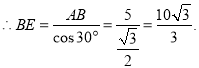
故答案为：．
练习册系列答案
相关题目
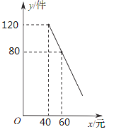
【题目】为倡导健康环保，自带水杯已成为一种好习惯，某超市销售甲，乙两种型号水杯，进价和售价均保持不变，其中甲种型号水杯进价为25元/个，乙种型号水杯进价为45元/个，下表是前两月两种型号水杯的销售情况：
时间 | 销售数量（个） | 销售收入（元）（销售收入＝售价×销售数量） | |
甲种型号 | 乙种型号 | ||
第一月 | 22 | 8 | 1100 |
第二月 | 38 | 24 | 2460 |
（1）求甲、乙两种型号水杯的售价；
（2）第三月超市计划再购进甲、乙两种型号水杯共80个，这批水杯进货的预算成本不超过2600元，且甲种型号水杯最多购进55个，在80个水杯全部售完的情况下设购进甲种号水杯a个，利润为w元，写出w与a的函数关系式，并求出第三月的最大利润．
