题目内容
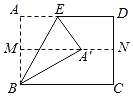
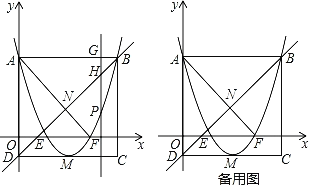
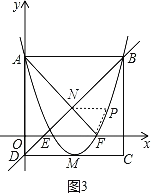
【题目】如图,抛物线y=x2+bx+c经过A (0,3),B (4,3)两点,与x轴交于点E,F,以AB为边作矩形ABCD,其中CD边经过抛物线的项点M,点P是抛物线上一动点(点P不与点A,B重合),过点P作y轴的平行线1与直线AB交于点G,与直线BD交于点H,连接AF交直线BD于点N.
(1)求该抛物线的解析式以及顶点M的坐标;
(2)当线段PH=2GH时,求点P的坐标;
(3)在抛物线上是否存在点P,使得以点P,E,N,F为顶点的四边形是平行四边形?若存在,请求出点P的坐标;若不存在,请说明理由.
【答案】(1)y=x2﹣4x+3,顶点M的坐标为(2,﹣1);(2)点P的坐标为(﹣1,8)或(3,0);(3)存在点P(2,﹣1)时,使得以点P,E,N,F为顶点的四边形是平行四边形.
【解析】
(1)根据抛物线y=x2+bx+c经过A(0,3),B(4,3)两点,可以求得该抛物线的解析式,然后化为顶点式,即可得到顶点M的坐标;
(2)根据题意,可以表示出线段PH和GH的长,然后即可得到点P的坐标;
(3)根据题意,画出相应的图象,然后利用分类讨论的方法即可得到点P的坐标.
解:(1)∵抛物线y=x2+bx+c经过A(0,3),B(4,3)两点,
∴![]() 得
得![]() ,
,
即该抛物线的解析式为y=x2﹣4x+3,
∵y=x2﹣4x+3=(x﹣2)2﹣1,
∴顶点M的坐标为(2,﹣1);
(2)∵四边形ABCD是矩形,且CD边经过抛物线的顶点M(2,﹣1),
∴D(0,﹣1),
设直线BD的解析式为y=kx+b,
∵直线BD经过点B(4,3),D(0,﹣1),
∴![]() ,
,
解得,![]() ,
,
∴直线BD的解析式为y=x﹣1,
∵点P为是抛物线上一动点,
∴设P(a,a2﹣4a+3),则G(a,3),H(a,a﹣1),
∴PH=|a2﹣4a+3﹣(a﹣1)|=|a2﹣5a+4|,GH=|3﹣(a﹣1)|=|4﹣a|,
∵PH=2GH,
∴|a2﹣5a+4|=2|4﹣a|,
解得,a1=﹣1,a2=3,a3=4,
∴P1(﹣1,8),P2(3,0),P3(4,3),
∵点P不与点A,B重合
∴P3(4,3)不符合要求,
∴当线段PH=2GH时,点P的坐标为P(﹣1,8)或P(3,0);
(3)当y=0时,0=x2﹣4x+3,得x1=3,x2=1,
则点E的坐标为(1,0),点F的坐标为(3,0),
∵A(0,3),F(3,0),
∴直线AF的解析式为y=﹣x+3,
联立![]() ,得
,得![]() ,
,
∴N(2,1),
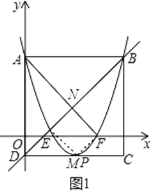
如图1所示,当点P在直线EF下方时,
∵M(2,﹣1),N(2,1),E(1,0),F(3,0),
∴MN与EF互相垂直平分,
∴当点P在点M的位置时,四边形PENF是平行四边形,
此时P(2,﹣1);
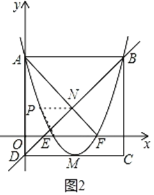
如图2所示,当点P在点E的左侧时,
若四边形PEFN是平行四边形,则P(0,1),
∵抛物线经过点A(0,3),
∴P(0,1)不符合实际,舍去;
如图3所示,当点P在点F的右侧时,
若四边形PFEN是平行四边形,则P(4,1),
∵抛物线经过点B(4,3),
∴P(4,1)不符合实际,舍去;
综上所述,存在点P(2,﹣1)时,使得以点P,E,N,F为顶点的四边形是平行四边形.

 阅读快车系列答案
阅读快车系列答案