题目内容
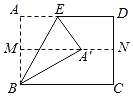
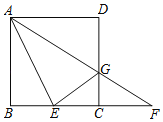
【题目】如图,在正方形ABCD中,点E在BC边上,连接AE,∠DAE的平分线AG与CD边交于点G,与BC的延长线交于点F.设![]() =λ(λ>0).
=λ(λ>0).
(1)若AB=2,λ=1,求线段CF的长.
(2)连接EG,若EG⊥AF,
①求证:点G为CD边的中点.
②求λ的值.
【答案】(1)![]() ﹣1;(2)①见解析;②λ=
﹣1;(2)①见解析;②λ=![]()
【解析】
(1)根据AB=2,λ=1,可以得到BE、CE的长,然后根据正方形的性质,可以得到AE的长,再根据平行线的性质和角平分线的性质,可以得到EF的长,从而可以得到线段CF的长;
(2)①要证明点G为CD边的中点,只要证明△ADG≌△FGC即可,然后根据题目中的条件,可以得到△ADG≌△FGC的条件,从而可以证明结论成立;
②根据题意和三角形相似,可以得到CE和EB的比值,从而可以得到λ的值.
解:(1)∵在正方形ABCD中,AD∥BC,
∴∠DAG=∠F,
又∵AG平分∠DAE,
∴∠DAG=∠EAG,
∴∠EAG=∠F,
∴EA=EF,
∵AB=2,∠B=90°,点E为BC的中点,
∴BE=EC=1,
∴AE=![]() =
=![]() ,
,
∴EF=![]() ,
,
∴CF=EF﹣EC=![]() ﹣1;
﹣1;
(2)①证明:∵EA=EF,EG⊥AF,
∴AG=FG,
在△ADG和△FCG中
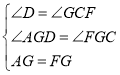 ,
,
∴△ADG≌△FCG(AAS),
∴DG=CG,
即点G为CD的中点;
②设CD=2a,则CG=a,
由①知,CF=DA=2a,
∵EG⊥AF,∠GDF=90°,
∴∠EGC+∠CGF=90°,∠F+∠CGF=90°,∠ECG=∠GCF=90°,
∴∠EGC=∠F,
∴△EGC∽△GFC,
∴![]() ,
,
∵GC=a,FC=2a,
∴![]() ,
,
∴![]() ,
,
∴EC=![]() a,BE=BC﹣EC=2a﹣
a,BE=BC﹣EC=2a﹣![]() a=
a=![]() a,
a,
∴λ=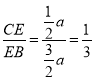 .
.

练习册系列答案
相关题目