Question

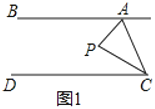
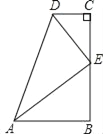
【题目】如图，∠B＝∠C＝90°，E是BC的中点，DE平分∠ADC，求证：

（1）AE是∠DAB的平分线；

（2）AE⊥DE．

Answer 1

【答案】(1)见解析;(2)见解析

【解析】

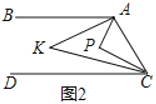
（1）过点E作EF⊥AD于点F，由角平分线的性质可知EF＝CE，由于E是BC的中点，所以CE＝EB，所以EF＝EB，再由角平分线的判定定理可知AE是∠DAB的平分线；

（2）由于AE是∠DAB的平分线，DE平分∠ADC，所以∠ADE＝ ∠ADC，∠DAE＝∠DAB，所以∠ADE+∠DAE＝×180°＝90°，从而可知AE⊥DE．

解：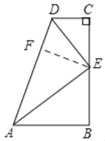

（1）过点E作EF⊥AD于点F，

∵DE平分∠ADC，CE⊥DC，EF⊥DA，

∴EF＝CE，

∵E是BC的中点，

∴CE＝EB，

∴EF＝EB，

∵EF⊥AD，EB⊥AB，

∴AE是∠DAB的平分线；

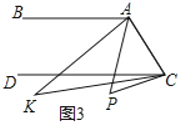
（2）∵AE是∠DAB的平分线，DE平分∠ADC，

∴，，

∵CD∥AB，

∴∠ADC+∠DAB＝180°，

∴∠ADE+∠DAE＝×180°＝90°，

∴∠DEA＝90°，

∴AE⊥DE．