题目内容
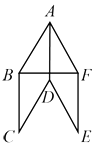
【题目】如图,小明将两块完全相同的直角三角形纸片的直角顶点C叠放在一起,若保持△BCD不动,将△ACE绕直角顶点C旋转.
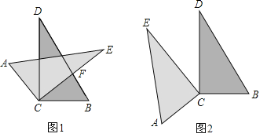
(1)如图1,如果CD平分∠ACE,那么CE是否平分∠BCD?答:______(填写“是”或“否”);
(2)如图1,若∠DCE=35,则∠ACB=______;若∠ACB=140,则∠DCE=______;
(3)当△ACE绕直角顶点C旋转到如图1的位置时,猜想∠ACB与∠DCE的数量关系,并说明理由;
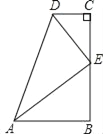
(4)当△ACE绕直角顶点C旋转到如图2的位置时,上述关系是否依然成立,请说明理由;
【答案】(1)是;(2)145°,40°;(3)∠ACB+∠DCE=180°,理由见解析;(4)成立,理由见解析
【解析】
(1)CD平分∠ACE,那么可得∠DCE=45°,进而求得∠BCF是45°,那么CE平分∠BCD;
(2)由∠DCE=35°可先求出∠ACD=55°,再结合∠ACB=∠DCB+∠ACD,∠BCD=90°即可求解;由∠ACB=140°,可先求出∠ACD从而求出∠DCE.
(3)根据∠ACE=∠DCB=90°,以及∠ACB=∠ACE+∠BCE,即可得出∠ACB+∠DCE=180°.
(4)根据周角定义,再结合已知条件,可以得出∠ACB+∠DCE=180°.
解:(1)∵CD平分∠ACE,∠ACE=90°,
∴∠ACD=∠DCE=45°,
∵∠DCB=90°,
∴∠ECB=90°∠DCE=45°
∴∠DCE=∠ECB,
∴CE平分∠DCB,
故答案为:是.
(2)∵∠ACD+∠DCE=90°,∠DCE=35°,
∴∠ACD=55°,
∴∠ACB=∠DCB+∠ACD=90°+55°=145°;
当∠ACB=140°,
∴∠ACD=∠ACB∠DCB=50°,
∴∠DCE=∠ACE∠ACD=40°.
故答案分别为:145°,40°.
(3)结论:∠ACB+∠DCE=180°,
理由:∵∠ACE=∠DCB=90°,∠ACB=∠ACE+∠BCE,
∴∠ACB+∠DCE=∠ACE+∠BCE+∠DCE=∠ACE+∠DCB=90°+90°=180°,
(4)成立.
理由∵∠ACE+∠DCB=180°,
又∵∠ACB+∠DCE+∠ACE+∠DCB=360°,∠ACE=∠DCB=90°,
∴∠ACB+∠DCE=360°(∠ACE+∠DCB)=180°.

 阅读快车系列答案
阅读快车系列答案