题目内容
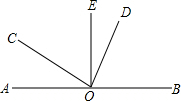如图所示，O是直线AB上的点，∠AOC=40°，OD平分∠BOC．（1）求∠BOD的度数．
（2）若OE⊥AB，分别求出∠DOE和∠COE的度数．
分析：（1）由平角的定义求得∠BOC=140°，再根据角平分线的定义求解即可解答；
（2）由垂线的定义可知∠BOE=∠AOE，根据互余的定义即可求得∠DOE和∠COE的度数．
（2）由垂线的定义可知∠BOE=∠AOE，根据互余的定义即可求得∠DOE和∠COE的度数．
解答：解：∵∠AOC=40°，
∴∠BOC=180°-∠AOC=180°-40°=140°，
∵OD平分∠BOC，
∴∠BOD=
∠BOC=70°．
（2）∵OE⊥AB，
∴∠BOE=∠AOE=90°，
∴∠DOE=90°-∠BOD=90°-70°=20°，
∠COE=90°-∠AOC=90°-40°=50°．
∴∠BOC=180°-∠AOC=180°-40°=140°，
∵OD平分∠BOC，
∴∠BOD=
| 1 |
| 2 |
（2）∵OE⊥AB，
∴∠BOE=∠AOE=90°，
∴∠DOE=90°-∠BOD=90°-70°=20°，
∠COE=90°-∠AOC=90°-40°=50°．
点评：此题主要考查了角平分线和垂线的定义，熟练掌握定义并进行计算是解答本题的关键．
练习册系列答案
周周清检测系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
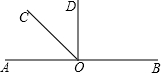如图所示，O是直线AB上一点，∠AOC=
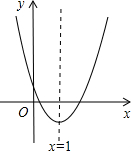（2013•广安）已知二次函数y=ax2+bx+c的图象如图所示，对称轴是直线x=1．下列结论：
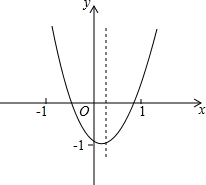已知抛物线y=ax2+bx+c（a≠0）在平面直角坐标系中的位置如图所示，对称轴是直线
0°．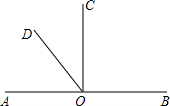
如图所示，0是直线AB上一点，0C是∠AOB的平分线．