题目内容
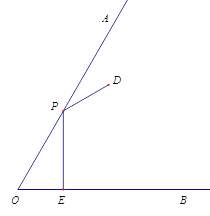
【题目】如图，已知∠AOB=60°，点P为射线OA上的一个动点，过点P作PE⊥OB，交OB 于点E，点D在∠AOB内，且满足∠DPA=∠OPE，DP+PE=6.
（1）当DP=PE时，求DE的长；
（2）在点P的运动过程中，请判断是否存在一个定点M，使得
的值不变？并证明你的判断.
【答案】（1）DE=3
；（2）当M点在射线OA上且满足OM=2时，
的值不变，始终为1.理由见解析.
【解析】
（1）作PF⊥DE交DE于F．由直角三角形的两锐角互余得到∠OPE=30°，在由平角的定义，得出∠EPD=120°．然后解三角形DPE即可得出结论．
（2）当点P与点M不重合时，延长EP到K使得PK=PD．可以证明△KPM≌△DPM，得到MK=MD．作ML⊥OE于L，MN⊥EK于N．解Rt△MLO得到ML的长，易证四边形MNEL为矩形，得到EN=ML=3．通过证明MK=ME，得到ME=MK=MD，即可得到=1．
当点P与点M重合时，结论也成立．
（1）作PF⊥DE交DE于F．
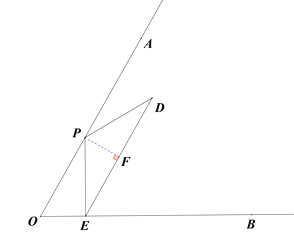
∵PE⊥BO，∠AOB=60°，∴∠OPE=30°，∴∠DPA=∠OPE=30°，∴∠EPD=120°．
∵DP=PE，DP+PE=6，∴∠PDE=30°，PD=PE=3，∴DF=PDcos30°=
，∴DE=2DF=
．
（2）当M点在射线OA上且满足OM=
时，的值不变，始终为1．理由如下：
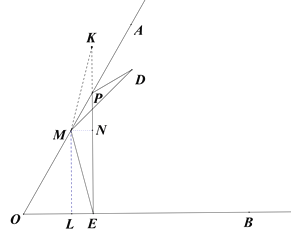
①当点P与点M不重合时，延长EP到K使得PK=PD，连接MK．
∵∠DPA=∠OPE，∠OPE=∠KPA，∴∠KPA=∠DPA，∴∠KPM=∠DPM．
∵PK=PD，PM是公共边，∴△KPM≌△DPM，∴MK=MD．
作ML⊥OE于L，MN⊥EK于N．
∵MO=，∠MOL=60°，∴ML=MOsin60°=3．
∵PE⊥BO，ML⊥OE，MN⊥EK，∴四边形MNEL为矩形，∴EN=ML=3．
∵EK=PE+PK=PE+PD=6，∴EN=NK．
∵MN⊥EK，∴MK=ME，∴ME=MK=MD，即=1．
②当点P与点M重合时，由上述过程可知结论成立．
