Question

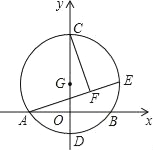
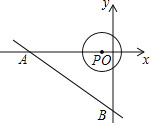
【题目】在直角坐标平面内，点O在坐标原点，已知点A（3，1）、B（2，0）、C（4，﹣2）．

（1）求证：△AOB∽△OCB；

（2）求∠AOC的度数．

Answer 1

【答案】（1）证明见解析；（2）∠AOC＝45°．

【解析】

（1）分别求出AB，OB，BC的长，即可求得＝，结合∠ABO＝∠CBO＝135°即可判定；

（2）根据相似三角形对应角相等可得∠BOC＝∠A，求出∠AOC＝∠AOB+∠A即可解题．

解：如图：

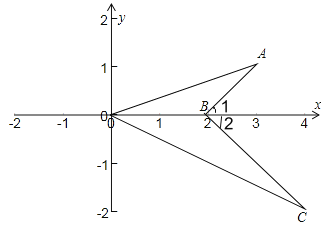
（1）∵A（3，1）、B（2，0）、C（4，﹣2）．

∴AB＝，BC＝，OB＝2，

∴＝，

∵∠1＝∠2＝45°，

∴∠ABO＝∠CBO＝135°，

∴△AOB∽△OCB；

（2）∵△AOB∽△OCB，

∴∠BOC＝∠A，

∵∠AOC＝∠AOB+∠BOC＝∠AOB+∠A，

∴∠AOC＝180°－135°＝45°．