题目内容
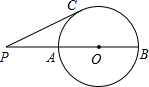
如图，AB是⊙O的直径，BC是一条弦，连接OC并延长至点P，使PC=BC，∠BOC=60°．
（1）求证：PB是⊙O的切线；
（2）若⊙O的半径为1，且AB、PB的长是方程x2+bx+c=0的两根，求b、c的值．
（1）求证：PB是⊙O的切线；
（2）若⊙O的半径为1，且AB、PB的长是方程x2+bx+c=0的两根，求b、c的值．
（1）证明：∵PC=BC，
∴∠P=∠CBP，
又∵OB=OC，∠BOC=60°，
∴△BOC是等边三角形，
∴∠OCB=∠BOC=60°，
又∠OCB=∠P+∠PBC，
∴∠P=∠CBP=30°，
在△BOP中，∠P=30°，∠BOP=60°，
∴∠OBP=90°，
∴BP是⊙O的切线；
（2）∵OB=1，∠P=30°，
∴AB=2，BP=
，
又∵AB、BP是方程x2+bx+c=0的两根，
∴AB+BP=-b，AB•BP=c，
∴b=-2-
，c=2
．
∴∠P=∠CBP，
又∵OB=OC，∠BOC=60°，
∴△BOC是等边三角形，
∴∠OCB=∠BOC=60°，
又∠OCB=∠P+∠PBC，
∴∠P=∠CBP=30°，
在△BOP中，∠P=30°，∠BOP=60°，
∴∠OBP=90°，
∴BP是⊙O的切线；
（2）∵OB=1，∠P=30°，
∴AB=2，BP=
| 3 |
又∵AB、BP是方程x2+bx+c=0的两根，
∴AB+BP=-b，AB•BP=c，
∴b=-2-
| 3 |
| 3 |
练习册系列答案
优百分课时互动系列答案
开心蛙状元作业系列答案
相关题目
且与BC所在直线相交？
