题目内容
如图,点O是矩形ABCD的中心,E是AB上的点,沿CE折叠后,点B恰好与点O重合.若BC=3,则折痕CE的长为_____________________.


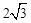 .
.试题分析:先根据图形翻折变换的性质求出AC的长,再由勾股定理及等腰三角形的判定定理即可得出结论:
∵△CEO是△CEB翻折而成,∴BC=OC,BE=OE.
∵O是矩形ABCD的中心,∴OE是AC的垂直平分线,AC=2BC=2×3=6.
∴AE=CE,
在Rt△ABC中,
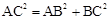 ,
,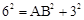 ,解得AB=
,解得AB=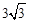 .
.在Rt△AOE中,设OE=x,则AE=
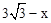 ,
,∴
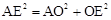 ,即
,即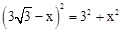 ,解得x=
,解得x=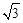 .
.∴EC="AE="
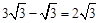 .
.
练习册系列答案
相关题目
 .
.
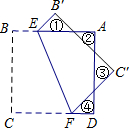

 经过点A,作AB⊥x轴于点B,将△ABO绕点B顺时针旋转
经过点A,作AB⊥x轴于点B,将△ABO绕点B顺时针旋转 得到△BCD,若点B的坐标为(2,0),则点C的坐标为( )
得到△BCD,若点B的坐标为(2,0),则点C的坐标为( )




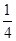 BD;其中正确结论的是( )
BD;其中正确结论的是( )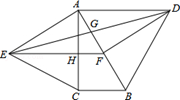
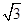 ,则AB的长为 .
,则AB的长为 .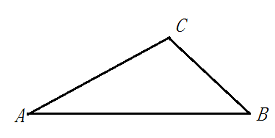
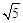 ,0),B(
,0),B(