题目内容
【题目】已知边长为1的正方形ABCD中, P是对角线AC上的一个动点(与点A、C不重合),过点P作PE⊥PB ,PE交射线DC于点E,过点E作EF⊥AC,垂足为点F.
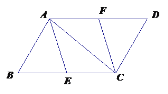
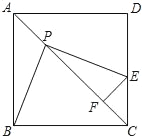
(1)当点E落在线段CD上时(如图),
①求证:PB=PE;
②在点P的运动过程中,PF的长度是否发生变化?若不变,试求出这个不变的值,若变化,试说明理由;
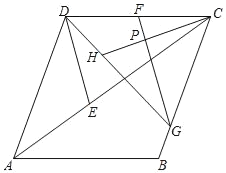
(2)当点E落在线段DC的延长线上时,在备用图上画出符合要求的大致图形,并判断上述(1)中的结论是否仍然成立(只需写出结论,不需要证明);
(3)在点P的运动过程中,△PEC能否为等腰三角形?如果能,试求出AP的长,如果不能,试说明理由.
【答案】(1)①证明见解析;②点PP在运动过程中,PF的长度不变,值为![]() ;(2)画图见解析,成立 ;(3)能,1.
;(2)画图见解析,成立 ;(3)能,1.
【解析】分析:(1)①过点P作PG⊥BC于G,过点P作PH⊥DC于H,如图1.要证PB=PE,只需证到△PGB≌△PHE即可;②连接BD,如图2.易证△BOP≌△PFE,则有BO=PF,只需求出BO的长即可.
(2)根据条件即可画出符合要求的图形,同理可得(1)中的结论仍然成立.
(3)可分点E在线段DC上和点E在线段DC的延长线上两种情况讨论,通过计算就可求出符合要求的AP的长.
详解:(1)①证明:过点P作PG⊥BC于G,过点P作PH⊥DC于H,如图1.
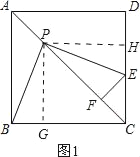
∵四边形ABCD是正方形,PG⊥BC,PH⊥DC,
∴∠GPC=∠ACB=∠ACD=∠HPC=45°.
∴PG=PH,∠GPH=∠PGB=∠PHE=90°.
∵PE⊥PB即∠BPE=90°,
∴∠BPG=90°﹣∠GPE=∠EPH.
在△PGB和△PHE中,
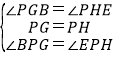 ,
,
∴△PGB≌△PHE(ASA),
∴PB=PE.
②连接BD,如图2.
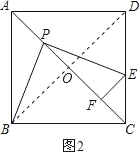
∵四边形ABCD是正方形,∴∠BOP=90°.
∵PE⊥PB即∠BPE=90°,
∴∠PBO=90°﹣∠BPO=∠EPF.
∵EF⊥PC即∠PFE=90°,
∴∠BOP=∠PFE.
在△BOP和△PFE中,
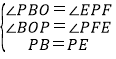
∴△BOP≌△PFE(AAS),
∴BO=PF.
∵四边形ABCD是正方形,
∴OB=OC,∠BOC=90°,
∴BC=![]() OB.
OB.
∵BC=1,∴OB=![]() ,
,
∴PF=![]() .
.
∴点PP在运动过程中,PF的长度不变,值为![]() .
.
(2)当点E落在线段DC的延长线上时,符合要求的图形如图3所示.
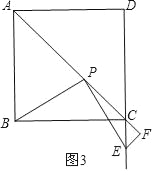
同理可得:PB=PE,PF=![]() .
.
(3)①若点E在线段DC上,如图1.
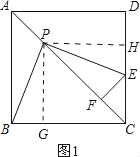
∵∠BPE=∠BCE=90°,∴∠PBC+∠PEC=180°.
∵∠PBC<90°,∴∠PEC>90°.
若△PEC为等腰三角形,则EP=EC.
∴∠EPC=∠ECP=45°,
∴∠PEC=90°,与∠PEC>90°矛盾,
∴当点E在线段DC上时,△PEC不可能是等腰三角形.
②若点E在线段DC的延长线上,如图4.

若△PEC是等腰三角形,
∵∠PCE=135°,
∴CP=CE,
∴∠CPE=∠CEP=22.5°.
∴∠APB=180°﹣90°﹣22.5°=67.5°.
∵∠PRC=90°+∠PBR=90°+∠CER,
∴∠PBR=∠CER=22.5°,
∴∠ABP=67.5°,
∴∠ABP=∠APB.
∴AP=AB=1.
∴AP的长为1.