Question

【题目】已知：如图，在□ABCD中，E、F分别为BC、AD的中点．

（1）试判断四边形AECF是什么四边形？为什么？

（2）当AB⊥AC时，四边形AECF是什么四边形？

（3）结合图形，请你添加一个条件，使其与原已知条件共同能推出四边形AECF是矩形．

Answer 1

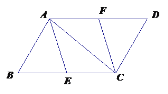
【答案】（1）四边形AECF是平行四边形，理由见解析；（2）当AB⊥AC时四边形AECF是菱形，理由见解析；（3）添加的条件是∠AEC=90°，理由见解析.

【解析】

（1）根据平行四边形的性质推出AD∥BC，AD=BC，再求出AF=CE，AF∥CE，即可得到答案；

（2）连接EF，易证四边形ABEF是平行四边形，得到EF∥AB，推出EF⊥AC，故平行四边形AECF是菱形；

（3）根据矩形的判定即可推出答案．

（1）四边形AECF是平行四边形．理由如下：

∵四边形ABCD是平行四边形，

∴AD∥BC，AD=BC，

∵E、F分别是BC、AD的中点，

∴AF=AD，CE=BC，

∴AF=CE，AF∥CE，

∴四边形AECF是平行四边形；

（2）当AB⊥AC时，四边形AECF是菱形．

理由是：连接EF，

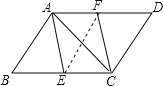
∵四边形ABCD是平行四边形，

∴AD∥BC，AD=BC，

∵E、F分别是BC、AD的中点，

∴AF=AD，BE=BC，

∴AF=BE，AF∥BE，

∴四边形AFEB是平行四边形，

∴AB∥EF，

∵AB⊥AC，

∴EF⊥AC，

∵由（1）知：四边形AECF是平行四边形，

∴平行四边形AECF是菱形（对角线互相垂直的平行四边形是菱形）；

（3）添加的条件是∠AEC=90°．

理由是：∵四边形AECF是平行四边形，∠AEC=90°，

∴平行四边形AECF是矩形．