题目内容
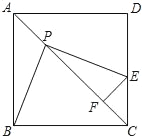
【题目】数学活动课上,励志学习小组对有一内角为120°的平行四边形ABCD(∠BAD=120°)进行探究:将一块含60°的直角三角板如图放置在平行四边形ABCD所在平面内旋转,且60°角的顶点始终与点C重合,较短的直角边和斜边所在的两直线分别交线段AB,AD于点E,F(不包括线段的端点).
(1)初步尝试
如图1,若AD=AB,求证:①△BCE≌△ACF,②AE+AF=AC;
(2)类比发现
如图2,若AD=2AB,过点C作CH⊥AD于点H,求证:AE=2FH;
在证明这道题时,励志学习小组成员小颖同学进行如下书写,请你将此证明过程补充完整
证明:设DH=x,由由题意,CD=2x,CH=![]() x,
x,
∴AD=2AB=4x,
∴AH=AD﹣DH=3x,
∵CH⊥AD,
∴AC=![]() =2
=2![]() x,
x,
(3)深入探究
在(2)的条件下,励志学习小组成员小漫同学探究发现![]() ,试判断小漫同学的结论是否正确,并说明理由
,试判断小漫同学的结论是否正确,并说明理由

【答案】(1)①见解析,②见解析;(2)见解析;(3)正确
【解析】(1)先证△ABC,△ACD都是等边三角形,再证△BCE和△ACF全等即可;
(2)先证△ACE∽△HCF,再利用相似三角形的性质即可得出答案;
(3)利用(2)中证得的结论利用等量代换即可得出答案.
解:(1)①∵四边形ABCD是平行四边形,∠BAD=120°,
∴∠D=∠B=60°,
∵AD=AB,
∴△ABC,△ACD都是等边三角形,
∴∠B=∠CAD=60°,∠ACB=60°,BC=AC,
∵∠ECF=60°,
∴∠BCE+∠ACE=∠ACF+∠ACE=60°,
∴∠BCE=∠ACF,
在△BCE和△ACF中,
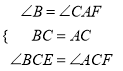 ,
,
∴△BCE≌△ACF.
②∵△BCE≌△ACF,
∴BE=AF,
∴AE+AF=AE+BE=AB=AC.
(2)∴AC2+CD2=AD2,
∴∠ACD=90°,
∴∠BAC=∠ACD=90°,
∴∠CAD=30°,
∴∠ACH=60°,
∵∠ECF=60°,
∴∠HCF=∠ACE,
∴△ACE∽△HCF,
∴![]() =2,
=2,
∴AE=2FH.
(3)结论正确
如图2中,由(2)可知,设![]() ,则
,则![]() ,设
,设![]() ,则
,则![]() ,易知
,易知![]() ,∴
,∴![]() ,∴
,∴![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案