题目内容
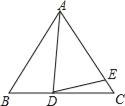
【题目】如图所示,在菱形ABCD中,AC是对角线,CD=CE,连接DE.
(1)若AC=16,CD=10,求DE的长.
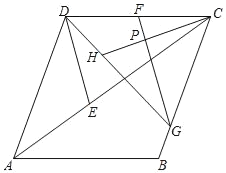
(2)G是BC上一点,若GC=GF=CH且CH⊥GF,垂足为P,求证:![]() DH=CF.
DH=CF.
【答案】(1)2![]() (2)见解析
(2)见解析
【解析】
(1)连接BD交AC于K.想办法求出DK,EK,利用勾股定理即可解决问题;
(2)证明:过H作HQ⊥CD于Q,过G作GJ⊥CD于J.想办法证明∠CDH=∠HGJ=45°,可得DH=![]() QH解决问题.
QH解决问题.
(1)解:连接BD交AC于K.
∵四边形ABCD是菱形,
∴AC⊥BD,AK=CK=8,
在Rt△AKD中,DK=![]() =6,
=6,
∵CD=CE,
∴EK=CE﹣CK=10﹣8=2,
在Rt△DKE中,DE=![]() =2
=2![]() .
.
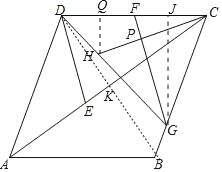
(2)证明:过H作HQ⊥CD于Q,过G作GJ⊥CD于J.
∵CH⊥GF,
∴∠GJF=∠CQH=∠GPC=90°,
∴∠QCH=∠JGF,
∵CH=GF,
∴△CQH≌△GJF(AAS),
∴QH=CJ,
∵GC=GF,
∴∠QCH=∠JGF=∠CGJ,CJ=FJ=![]() CF,
CF,
∵GC=CH,
∴∠CHG=∠CGH,
∴∠CDH+∠QCH=∠HGJ+∠CGJ,
∴∠CDH=∠HGJ,
∵∠GJF=∠CQH=∠GPC=90°,
∴∠CDH=∠HGJ=45°,
∴DH=![]() QH,
QH,
∴![]() DH=2QH=CF.
DH=2QH=CF.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目