Question

【题目】在矩形ABCD中 ，AB=8 , BC=6, 点P在边AB上。若将△DAP沿DP折叠 ，使点A落在矩形对角线上的点A，处，则AP的长为__________。

Answer 1

【答案】3或

【解析】①点A落在矩形对角线BD上，如图1所示。

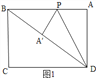
∵AB=8，AD=BC=6，∴BD=10，

根据折叠的性质,AD= =6,AP= ,∠A= =90°，∴=4，

设AP=x，则BP=8x，

∵ ，∴(8x) =x+4，解得：x=3，∴AP=3；

②点A落在矩形对角线AC上，如图2所示：

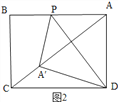
由折叠的性质可知PD垂直平分AA′，

∴∠BAC+∠=∠PDA+∠=90°.∴∠BAC=∠PDA.

∴tan∠BAC=tan∠PDA.∴.

∴AP= .综上所述AP的长为3或.

故答案为：3或.