Question

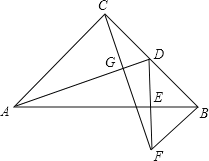
【题目】如图，已知等腰△ABC，∠BAC＝120°，AD⊥BC于D点，点P为BA延长线上一点，点O是线段AD上一点，若AC＝AO+AP．

（1）求证：∠APO＝∠OCA；

（2）求证：△OCP是等边三角形．

Answer 1

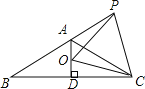
【答案】（1）见解析；（2）见解析

【解析】

（1）在AC上截取AE＝AP，连接PE，证出△APE是等边三角形，得出∠PEA＝∠APE＝∠PAE =60°，PE＝AP＝AE，证出AO＝EC，证明△OPA≌△CPE，得出∠APO＝∠EPC，OP＝CP，证明△OCP是等边三角形，得出∠OCP＝60°，即∠OCA+∠PCE＝60°，证出∠OCA＝∠EPC，即可得出结论；

（2）由（1）得出△OPA≌△CPE，得出∠APO＝∠EPC，OP＝CP，证出∠OPC＝60°，即可得出△OCP是等边三角形．

（1）证明：在AC上截取AE＝AP，连接PE，

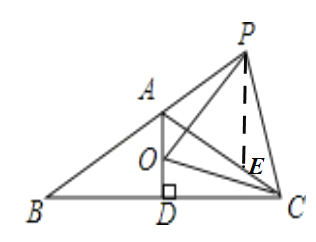
∵∠BAC＝120°，AD⊥BC

∵∠PAE＝180°﹣∠BAC＝60°，

∴△APE是等边三角形，

∴∠PEA＝∠APE＝∠PAE＝60°，PE＝AP＝AE，

∴∠PEC＝120°, ，

∵AC＝AO+AP,AC＝AE+EC，

∴AO＝EC，

在△OPA和△CPE中， ，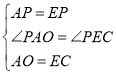

∴△OPA≌△CPE（SAS），

∴∠APO＝∠EPC，OP＝CP，

∴∠OPC＝∠OPE+∠EPC＝∠OPE+∠APO＝∠APE＝60°，

∴△OCP是等边三角形，

∴∠OCP＝60°，即∠OCA+∠PCE＝60°，

∵∠EPC+∠PCE＝∠AEP＝60°，

∴∠OCA＝∠EPC，

∴∠APO＝∠OCA；

（2）证明：由（1）得：△OPA≌△CPE（SAS），

∴∠APO＝∠EPC，OP＝CP，

∴∠OPC＝∠OPE+∠EPC＝∠OPE+∠APO＝∠APE＝60°，

∴△OCP是等边三角形．