Question

【题目】如图，四边形 ABCD 是矩形，把矩形沿直线 BD 拆叠，点 C 落在点 E 处，连接 DE， DE 与 AD 交于点 M．

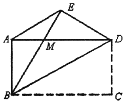
（1）证明四边形 ABDE 是等腰梯形；

（2）写出等腰梯形 ABDE 与矩形 ABCD 的面积大小关系，并证明你的结论．

Answer 1

【答案】（1）答案见解析；（2）等腰梯形ABDE小于矩形ABCD的面积

【解析】

（1）结合图形证△AMB≌△EMD，再结合图形的折叠关系可得答案．

（2） 由AE<BD,以及平行线间的距离相等，可得由于以及 可得结论.

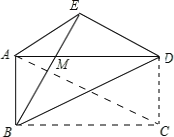
证明：(1)∵四边形ABCD是矩形，

∴AD=BE,AB=ED,AD∥BC.

∴△ADB≌△DBC≌△EDB,∠EBD=∠DBC,∠ADB=∠EBD.

∴DM=BM，AM=EM.

∴△AMB≌△EMD.

∴AB=DE.AM=EM，

∴∠EAM=∠AEM，

∵DM=BM，

∴∠BDM=∠MBD，

又∵∠AME=∠BMD，

∴∠EAD=∠MDB，

∴AE∥BD.

∵AE≠BD，

∴四边形ABDE是等腰梯形.

(2)∵

∵

∵AE<BD，

∴

∴

∴ 等腰梯形ABDE小于矩形ABCD的面积.