题目内容
【题目】已知,如图:在△ABC中,AC=3,BC=6,∠C=60![]() ;
;
(1)将△ABC绕着点C旋转,使点A落在直线BC上的点A′,点B落在B′,在下图中画出旋转后的△A′B′C.
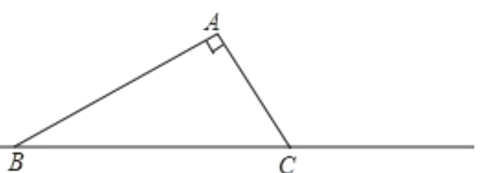
(2)直接写出A′B的长,A′B=___________.
【答案】(1)见详解;(2)3cm或9cm
【解析】
(1)利用∠C=60°和旋转的性质,将△ABC绕着点C顺时针旋转120°时,点A落在直线BC上的点A′,画出此时的△A′B′C;将△ABC绕着点C逆时针旋转60°时,点A落在直线BC上的点A′,画出此时的△A′B′C;
(2)利用(1)中的两个图形分类计算.
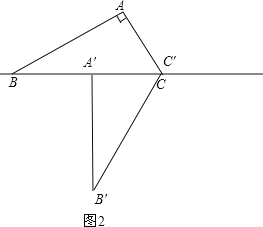
解:(1)如图1,如图2,△A′B′C为所作;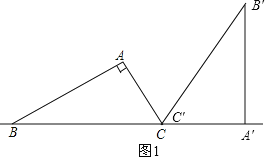
(2)将△ABC绕着点C顺时针旋转120°得到△A′B′C′,如图1,则CA′=CA=3cm,∴A′B=CB+CA′=9cm;
将△ABC绕着点C逆时针旋转60°得到△A′B′C′,如图2,则CA′=CA=3cm,
∴A′B=CB-CA′=3cm.
故A′B为3cm或9cm.

练习册系列答案
相关题目