题目内容
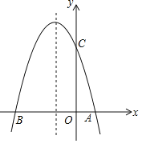
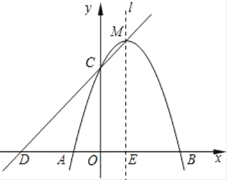
【题目】已知函数图象如图所示，根据图象可得：
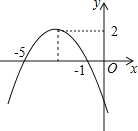
（1）抛物线顶点坐标_____．
（2）对称轴为_____．
（3）当_____时，y随着x得增大而增大
（4）当_____时，y＞0．
【答案】（﹣3，2） x＝﹣3 x＜﹣3 ﹣5＜x＜﹣1
【解析】
（1）根据抛物线的对称性即可求出顶点坐标的横坐标；
（2）由抛物线的顶点坐标的横坐标即可得到对称轴；
（3）观察图像即可；
（4）观察图像即可；
解：（1）如图所示，抛物线的对称轴方程是：
＝﹣3．
则抛物线的顶点坐标是（﹣3，2）．
故答案是：（﹣3，2）．
（2）由（1）知，抛物线的对称轴为直线x＝﹣3．
故答案是：x＝﹣3；
（3）如图所示，当x＜﹣3时，y随着x得增大而增大．
故答案是：x＜﹣3；
（4）如图所示，当﹣5＜x＜﹣1时，y＞0．
故答案是：﹣5＜x＜﹣1．
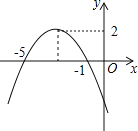
练习册系列答案
相关题目
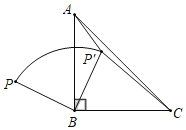
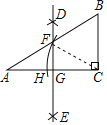
【题目】如图，一个滑道由滑坡（AB段）和缓冲带（BC段）组成，滑雪者在滑坡上滑行的距离y1（单位：m）和滑行时间t1（单位s）满足二次函数关系，并测得相关数据：
滑行时间t1/s | 0 | 1 | 2 | 3 | 4 |
滑行距离y1/s | 0 | 4.5 | 14 | 28.5 | 48 |
滑雪者在缓冲带上滑行的距离y2（单位：m）和滑行时间t2（单位：s）满足：y2=52t2﹣2t22，滑雪者从A出发在缓冲带BC上停止，一共用了23s．
（1）求y1和t1满足的二次函数解析式；
（2）求滑坡AB的长度．
