��Ŀ����
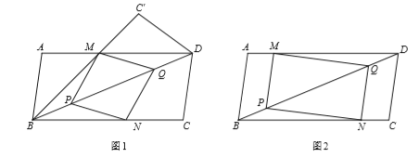
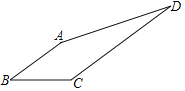
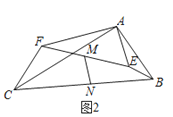
����Ŀ����ͼ1������ABC�У�AC��nAB����CAB��������E��F�ֱ���AB��AC����EF��BC������AEF�Ƶ�A˳ʱ����ת����ͼ2��λ�ã�����CF��BE��

��1����֤����ACF����ABE��
��2������M��N�ֱ���EF��BC���е㣬������90��ʱ����֤��BE2+CF2��4MN2��
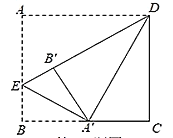
��3����ͼ3����M��N�ֱ���EF��BC����![]() ��
��![]() ��
��![]() ����n��
����n��![]() ������135����BE��
������135����BE��![]() ��ֱ��д��MN�ij���
��ֱ��д��MN�ij���
���𰸡���1������������2������������3��![]()
��������
��1��֤����CAF�ס�BAE���ɽ�����⣻
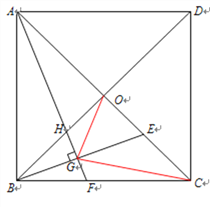
��2���ӳ�BE��CF���ӳ�����H������BF��ȡBF���е�J������NJ��JM����AC��BH�ڵ�O������֤��CF��BE�����������ε���λ�߶���֤����NJM��ֱ�������Σ����ù��ɶ������ɽ�����⣮
��3����ͼ3�У��ӳ�BE��CF���ӳ�����H������BF����FB��ȡһ��J��ʹ��FJ��JB��1��2������NJ��JM��֤����MJN��45����NJ��![]() ��MJ��
��MJ��![]() ����ͼ4�У�����NJM�У���MK��NJ��K����ֱ�����������MN���ɣ�
����ͼ4�У�����NJM�У���MK��NJ��K����ֱ�����������MN���ɣ�
��1��֤����
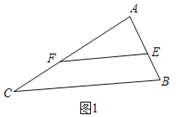
����ͼ1�У�
��EF��BC��
��![]() ��
��
��![]() ��
��
��ͼ2�У�
�ߡ�CAB����EAF��
���CAF����BAE��
��![]() ��
��
���CAF�ס�BAE��
���ACF����ABE��
��2��֤������ͼ2�У��ӳ�BE��CF���ӳ�����H������BF��ȡBF���е�J������NJ��JM����AC��BH�ڵ�O��
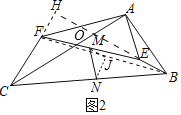
�ߡ�OCH����OBA����COH����BOA��
���H����OAB��90����
��CF��BE��
��CN��BN��FJ��JB��
��JN��CF��JN��![]() CF��
CF��
��FM��ME��FJ��JB��
��MJ��BE��MJ��![]() BE��
BE��
��CF��BE��
��NJ��JM��
���NJM��90����
��JN2+JM2��MN2��
�ࣨ![]() CF��2+��
CF��2+��![]() BE��2��MN2��
BE��2��MN2��
��BE2+CF2��4MN2��
��3���⣺��ͼ3�У��ӳ�BE��CF���ӳ�����H������BF����FB��ȡһ��J��ʹ��FJ��JB��1��2������NJ��JM��
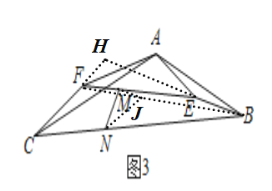
ͬ����֤��H����CAB��135����
��CN��BN��FJ��JB��1��2��
��NJ��CF��NJ��![]() CF��
CF��
��FM��ME��FJ��JB��1��2��
��MJ��BE��MJ��![]() BE��
BE��
���MJN�С�MJN�����Ϊ135����
���MJN��45����
������BE��![]() ��CF��2��
��CF��2��
��NJ��![]() ��MJ��
��MJ��![]() ��
��
��ͼ4�У�����NJM�У���MK��NJ��K��
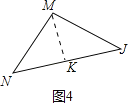
�ߡ�J����JMK��45����MJ��![]() ��
��
��MK��KJ��![]() ��
��
��NK��NJ��KJ��1��
��MN��![]() =
=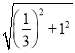 ��
��![]() ��
��