题目内容
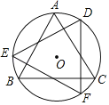
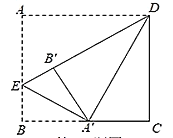
【题目】如图,在矩形![]() 中,
中,![]() .将
.将![]() 向内翻折,点
向内翻折,点 ![]() 落在
落在![]() 上,记为
上,记为![]() ,折痕为
,折痕为![]() .若将
.若将![]() 沿
沿![]() 向内翻折,点
向内翻折,点![]() 恰好 落在
恰好 落在![]() 上,记为
上,记为![]() ,则
,则![]() 的长为( )
的长为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】B
【解析】
首先根据矩形和翻折的性质得出△AED≌△A'ED,△A'BE≌△A'B'E,∠A'B'E=∠B=∠A'B'D=90°,∠AED=∠A'ED,∠A'EB=∠A'EB',BE=B'E,进而得出∠AED=∠A'ED=∠A'EB=60°,∠ADE=∠A'DE=∠A'DC=30°,判定△DB'A'≌△DCA',DC=DB',得出AE,设AB=DC=x,利用勾股定理构建方程,即可得解.
∵四边形ABCD为矩形,
∴∠ADC=∠C=∠B=90°,AB=DC,
由翻折知,△AED≌△A'ED,△A'BE≌△A'B'E,∠A'B'E=∠B=∠A'B'D=90°,
∴∠AED=∠A'ED,∠A'EB=∠A'EB',BE=B'E,
∴∠AED=∠A'ED=∠A'EB=![]() ×180°=60°,
×180°=60°,
∴∠ADE=90°﹣∠AED=30°,∠A'DE=90°﹣∠A'EB=30°,
∴∠ADE=∠A'DE=∠A'DC=30°,
又∵∠C=∠A'B'D=90°,DA'=DA',
∴△DB'A'≌△DCA'(AAS),
∴DC=DB',
在Rt△AED中,
∠ADE=30°,AD=2,
∴AE=![]() ,
,
设AB=DC=x,则BE=B'E=x﹣![]()
∵AE2+AD2=DE2,
∴(![]() )2+22=(x+x﹣
)2+22=(x+x﹣![]() )2,
)2,
解得,x1=![]() (负值舍去),x2=
(负值舍去),x2=![]() ,
,
故答案为B.

 同步练习强化拓展系列答案
同步练习强化拓展系列答案【题目】数学活动课上,老师提出问题:如图1,有一张长![]() ,宽
,宽![]()
![]() 的长方形纸板,在纸板的四个角裁去四个相同的小正方形,然后把四边折起来,做成-一个无盖的盒子,问小正方形的边长为多少时,盒子的体积最大.下 面是探究过程,请补充完整:
的长方形纸板,在纸板的四个角裁去四个相同的小正方形,然后把四边折起来,做成-一个无盖的盒子,问小正方形的边长为多少时,盒子的体积最大.下 面是探究过程,请补充完整:
(1)设小正方形的边长为![]() ,体积为
,体积为![]() ,根据长方体的体积公式得到
,根据长方体的体积公式得到![]() 和
和![]() 的关系式 ;
的关系式 ;
(2)确定自变量![]() 的取值范围是
的取值范围是
(3)列出![]() 与
与![]() 的几组对应值.
的几组对应值.

| ··· |
|
|
|
|
|
|
|
|
|
|
| ··· |
|
|
|
|
|
|
|
|
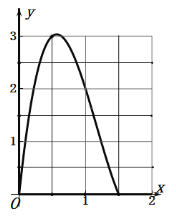
(4)在平面直角坐标系![]() 中,描出以补全后的表中各对对应值为坐标的点画出该函数的图象如图2,结合画出的函数图象,当小正方形的边长约为
中,描出以补全后的表中各对对应值为坐标的点画出该函数的图象如图2,结合画出的函数图象,当小正方形的边长约为 ![]() 时, 盒子的体积最大,最大值约为
时, 盒子的体积最大,最大值约为![]() .(估读值时精确到
.(估读值时精确到![]() )
)