Question

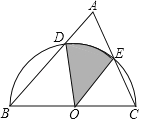
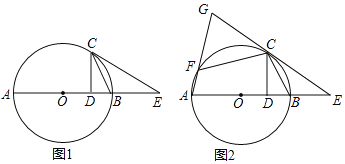
【题目】如图1，AB为⊙O的直径，C为⊙O上一点，连接CB，过C作CD⊥AB于点D，过点C作∠BCE，使∠BCE＝∠BCD，其中CE交AB的延长线于点E．

（1）求证：CE是⊙O的切线．

（2）如图2，点F在⊙O上，且满足∠FCE＝2∠ABC，连接AF井延长交EC的延长线于点G．

①试探究线段CF与CD之间满足的数量关系；

②若CD＝4，BD＝2，求线段FG的长．

Answer 1

【答案】（1）详见解析；（2）①CF＝2CD；②FG＝．

【解析】

（1）如图1，连接OC，根据等边对等角得：∠OBC＝∠OCB，由垂直定义得：∠OBC+∠BCD＝90°，根据等量代换可得：∠OCB+∠BCE＝90°，即OC⊥CE，可得结论；

（2）①如图2，过O作OH⊥CF于点H，证明△COH≌△COD，则CH＝CD，得CF＝2CD；

②先根据勾股定理求BC＝＝2，则CF＝2CD＝8，设OC＝OB＝x，则OD＝x﹣2，根据勾股定理列方程得：x2＝（x﹣2）2+42，可得x的值，证明△GFC∽△CBO，列比例式可得FG的长．

（1）证明：如图1，连接OC，

∵OB＝OC，

∴∠OBC＝∠OCB，

∵CD⊥AB，

∴∠OBC+∠BCD＝90°，

∵∠BCE＝∠BCD，

∴∠OCB+∠BCE＝90°，即OC⊥CE，

∴CE是⊙O的切线；

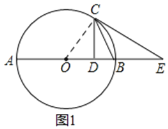
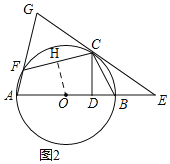
（2）解：①线段CF与CD之间满足的数量关系是：CF＝2CD，

理由如下：

如图2，过O作OH⊥CF于点H，

∴CF＝2CH，

∵∠FCE＝2∠ABC＝2∠OCB，且∠BCD＝∠BCE，

∴∠OCH＝∠OCD，

∵OC为公共边，

∴△COH≌△COD（AAS），

∴CH＝CD，

∴CF＝2CD；

②∵CD＝4，BD＝2，

∴BC＝＝2，由①得：CF＝2CD＝8，

设OC＝OB＝x，则OD＝x﹣2，

在Rt△ODC中，OC2＝OD2+CD2，

∴x2＝（x﹣2）2+42，

解得：x＝5，即OB＝5，

∵OC⊥GE，

∴∠OCF+∠FCG＝90°，

∵∠OCD+∠COD＝90°，∠FCO＝∠OCD，

∴∠GCF＝∠COB，

∵四边形ABCF为⊙O的内接四边形，

∴∠GFC＝∠ABC，

∴△GFC∽△CBO，

∴，

∴，

∴FG＝．