题目内容
【题目】如果一条直线把一个平面图形的面积分成相等的两部分,我们把这条直线称为这个平面图形的面积等分线.
问题探究
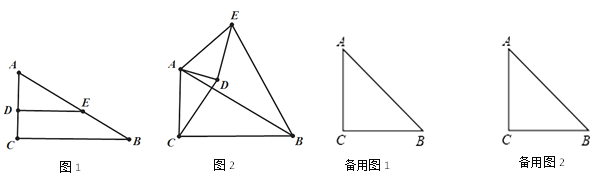
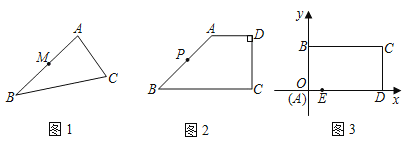
(1)如图1,△ABC中,点M是AB边的中点,请你过点M作△ABC的一条面积等分线;
(2)如图2,在四边形ABCD中,AD∥BC,CD⊥AD,AD=2,CD=4,BC=6,点P是AB的中点,点Q在CD上,试探究当CQ的长为多少时,直线PQ是四边形ABCD的一条面积等分线;
问题解决
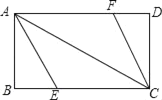
(3)如图3,在平面直角坐标系中,矩形ABCD是某公司将要筹建的花园示意图,A与原点重合,D、B分别在x轴、y轴上,其中AB=3,BC=5,出入口E在边AD上,且AE=1,拟在边BC、AB、CD、上依次再找一个出入口F、G、H,沿EF、GH修两条笔直的道路(路的宽度不计)将花园分成四块,在每一块内各种植一种花草,并要求四种花草的种植面积相等.请你求出此时直线EF和GH的函数表达式.
【答案】(1)详见解析;(2)当CQ的长为1时,直线PQ是四边形ABCD的一条面积等分线;(3)直线EF的解析式为y=x﹣1,直线GH的解析式为y=﹣![]() x+
x+![]() .
.
【解析】
(1)连接CM,得出△ACM的面积=△BCM的面积,得出CM是△ABC的一条面积等分线;
(2)连接PC,作AM⊥BC于M,PN⊥BC于N,则AM∥PN,四边形AMCD是矩形,求出PN是△ABM的中位线,得出PN=![]() AM=2,得出△BCP的面积=6,由题意得出四边形PBCQ的面积=
AM=2,得出△BCP的面积=6,由题意得出四边形PBCQ的面积=![]() 梯形ABCD的面积=8,得出△PCQ的面积=2=
梯形ABCD的面积=8,得出△PCQ的面积=2=![]() CQ×CN=
CQ×CN=![]() CQ×4,解得CQ=1即可;
CQ×4,解得CQ=1即可;
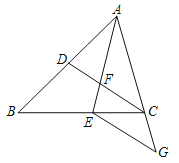
(3)连接AC、BD交于点P,证明△PCF≌△PAE(ASA),得出CF=AE=1,BF=5﹣1=4,得出E(1,0),F(4,3),由待定系数法求出直线EF的解析式为y=x﹣1;同理△BPG≌△DPH(ASA),得出BG=DH,求出H(5,![]() ),G(0,
),G(0,![]() ),由待定系数法求出直线GH的解析式为y=﹣
),由待定系数法求出直线GH的解析式为y=﹣![]() x+
x+![]() .
.
解:(1)连接CM,如图1所示:
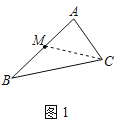
∵点M是AB边的中点,
∴△ACM的面积=△BCM的面积,
∴CM是△ABC的一条面积等分线;
(2)当CQ的长为1时,直线PQ是四边形ABCD的一条面积等分线;理由如下:
连接PC,作AM⊥BC于M,PN⊥BC于N,如图2所示:
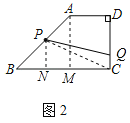
则AM∥PN,四边形AMCD是矩形,
∴AM=CD=4,CM=AD=2,
∴BM=BC﹣CM=4,
∵点P是AB的中点,
∴PN是△ABM的中位线,
∴PN=![]() AM=2,MN=
AM=2,MN=![]() BM=2,CN=NM+CM=4
BM=2,CN=NM+CM=4
∴△BCP的面积=![]() ×6×2=6,
×6×2=6,
∵梯形ABCD的面积=![]() (AD+BC)×CD=
(AD+BC)×CD=![]() (2+6)×4=16,直线PQ是四边形ABCD的一条面积等分线;
(2+6)×4=16,直线PQ是四边形ABCD的一条面积等分线;
∴四边形PBCQ的面积=![]() 梯形ABCD的面积=8,
梯形ABCD的面积=8,
∴△PCQ的面积=8﹣6=2=![]() CQ×CN=
CQ×CN=![]() CQ×4,
CQ×4,
解得:CQ=1,
即当CQ的长为1时,直线PQ是四边形ABCD的一条面积等分线;
(3)连接AC、BD交于点P,如图3所示:
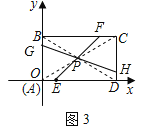
∵EF、GH将花园分成四块,且面积相等,
∴EF、GH经过点P,
∵四边形ABCD是矩形,
∴AD=BC=5,CD=AB=3,PA=PC,AD∥BC,
∴∠PCF=∠PAE,
在△PCF和△PAE中, ,
,
∴△PCF≌△PAE(ASA),
∴CF=AE=1,BF=5﹣1=4,
∴E(1,0),F(4,3),
设直线EF的解析式为y=kx+b,
把E(1,0),F(4,3)代入得:![]() ,
,
解得:![]() ,
,
∴直线EF的解析式为y=x﹣1;
同理:△BPG≌△DPH(ASA),
∴BG=DH,
由题意得:△PBG的面积=△PAE的面积,
∴![]() BG×
BG×![]() =
=![]() ×1×
×1×![]() ,
,
解得:BG=![]() ,
,
∴DH=BG=![]() ,
,
∴H(5,![]() ),AG=AB﹣BG=
),AG=AB﹣BG=![]() ,
,
∴G(0,![]() ),
),
设直线GH的解析式为y=ax+c,
把G(0,![]() ),H(5,
),H(5,![]() )代入得
)代入得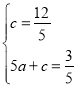 ,
,
解得: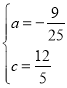 ,
,
∴直线GH的解析式为y=﹣![]() x+
x+![]() .
.

 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案【题目】为了了解我市中学生参加“科普知识”竞赛成绩的情况,随机抽查了部分参赛学生的成绩,整理并制作出如下的统计表和统计图,如图所示,请根据图表信息解答下列问题:
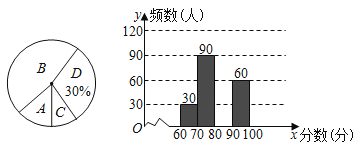
组别 | 分数段(分) | 频数 |
A组 | 60≤x<70 | 30 |
B组 | 70≤x<80 | 90 |
C组 | 80≤x<90 | m |
D组 | 90≤x<100 | 60 |
(1)本次调查的总人数为 人.
(2)补全频数分布直方图;
(3)若A组学生的平均分是65分,B组学生的平均分是75分,C组学生的平均分是85分,D出学生的平均分是95分,请你估计参加本次测试的同学们平均成绩是多少分?