Question

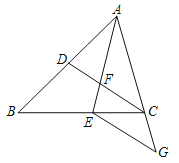
【题目】如图，在△ABC中，点D、E分别在边AB、BC上，AE与CD交于点F，若AE平分∠BAC，ABAF＝ACAE．

（1）求证：∠AFD＝∠AEC；

（2）若EG∥CD，交边AC的延长线于点G，求证：CDCG＝FCBD．

Answer 1

【答案】（1）详见解析；（2）详见解析．

【解析】

（1）先证△BAE∽△CAF，推出∠AEB＝∠AFC，由等角的补角相等可得出结论；

（2）先证明∠DCB＝∠CEG，∠G＝∠ACF＝∠B，推出△BDC∽△GCE，由相似三角形的性质可得出结论．

（1）证明：∵ABAF＝ACAE，

∴，

∵AE平分∠BAC，

∴∠BAE＝∠CAE，

∴△BAE∽△CAF，

∴∠AEB＝∠AFC，

∴180°﹣∠AEB＝180°﹣∠AFC，

∴∠AEC＝∠AFD；

（2）证明：∵∠CFE＝∠AFD＝∠CEF，

∴CE＝CF，

∵DC∥EG，

∴∠DCB＝∠CEG，∠G＝∠ACF＝∠B，

∴△BDC∽△GCE，

∴，

∴CDCG＝FCBD．