题目内容
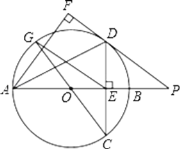
【题目】如图,Rt△ABC中,∠C=90°,E是AB边上一点,D是AC边上一点,且点D不与A、C重合,ED⊥AC.
(1)当sinB=![]() 时,
时,
①求证:BE=2CD.
②当△ADE绕点A旋转到如图2的位置时(45°<∠CAD<90°).BE=2CD是否成立?若成立,请给出证明;若不成立.请说明理由.
(2)当sinB=![]() 时,将△ADE绕点A旋转到∠DEB=90°,若AC=10,AD=2
时,将△ADE绕点A旋转到∠DEB=90°,若AC=10,AD=2![]() ,求线段CD的长.
,求线段CD的长.
【答案】(1)①证明见解析;②BE=2CD成立.理由见解析;(2)2![]() 或4
或4![]() .
.
【解析】
(1)①作EH⊥BC于点H,由sinB=![]() 可得∠B=30°,∠A=60°,根据ED⊥AC可证明四边形CDEH是矩形,根据矩形的性质可得EH=CD,根据正弦的定义即可得BE=2CD;
可得∠B=30°,∠A=60°,根据ED⊥AC可证明四边形CDEH是矩形,根据矩形的性质可得EH=CD,根据正弦的定义即可得BE=2CD;
②根据旋转的性质可得∠BAC=∠EAD,利用角的和差关系可得∠CAD=∠BAE,根据![]() =
=![]() 可证明△ACD∽△ABE,及相似三角形的性质可得
可证明△ACD∽△ABE,及相似三角形的性质可得![]() ,进而可得BE=2CD;
,进而可得BE=2CD;
(2)由sinB=![]() 可得∠ABC=∠BAC=∠DAE=45°,根据ED⊥AC可得AD=DE,AC=BC,如图,分两种情况讨论,通过证明△ACD∽△ABE,求出CD的长即可.
可得∠ABC=∠BAC=∠DAE=45°,根据ED⊥AC可得AD=DE,AC=BC,如图,分两种情况讨论,通过证明△ACD∽△ABE,求出CD的长即可.
(1)①作EH⊥BC于点H,
∵Rt△ABC中,∠C=90°,sinB=![]() ,
,
∴∠B=30°,
∴∠A=60°,
∵ED⊥AC
∴∠ADE=∠C=90°,
∴四边形CDEH是矩形,即EH=CD.
∴在Rt△BEH中,∠B=30°
∴BE=2EH
∴BE=2CD.
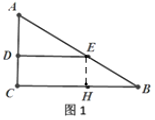
②BE=2CD成立.
理由:∵△ADE绕点A旋转到如图2的位置,
∴∠BAC=∠EAD=60°,
∴∠BAC+∠BAD=∠EAD+∠BAD,即∠CAD=∠BAE,
∵AC:AB=1:2,AD:AE=1:2,
∴![]() ,
,
∴△ACD∽△ABE,
∴![]() ,
,
又∵Rt△ABC中,![]() =2,
=2,
∴![]() =2,即BE=2CD.
=2,即BE=2CD.
(2)∵sinB=![]() ,
,
∴∠ABC=∠BAC=∠DAE=45°,
∵ED⊥AC,
∴∠AED=∠BAC=45°,
∴AD=DE,AC=BC,
将△ADE绕点A旋转,∠DEB=90°,分两种情况:
①如图所示,过A作AF⊥BE于F,则∠F=90°,
当∠DEB=90°时,∠ADE=∠DEF=90°,
又∵AD=DE,
∴四边形ADEF是正方形,
∴AD=AF=EF=2![]() ,
,
∵AC=10=BC,
∴AB=10![]() ,
,
∴Rt△ABF中,BF=![]() =6
=6![]() ,
,
∴BE=BF﹣EF=4![]() ,
,
又∵△ABC和△ADE都是直角三角形,
且∠BAC=∠EAD=45°,
∴∠CAD=∠BAE,
∵AC:AB=1:![]() ,AD:AE=1:
,AD:AE=1:![]() ,
,
∴![]() ,
,
∴△ACD∽△ABE,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
∴CD=2![]() ;
;

②如图所示,过A作AF⊥BE于F,则∠AFE=∠AFB=90°,
当∠DEB=90°,∠DEB=∠ADE=90°,
又∵AD=ED,
∴四边形ADEF是正方形,
∴AD=EF=AF=2![]() ,
,
又∵AC=10=BC,
∴AB=10![]() ,
,
∴Rt△ABF中,BF=![]() =6
=6![]() ,
,
∴BE=BF+EF=8![]() ,
,
又∵△ACD∽△ABE,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
∴CD=4![]() ,
,
综上所述,线段CD的长为2![]() 或4
或4![]() .
.

 阅读快车系列答案
阅读快车系列答案