题目内容
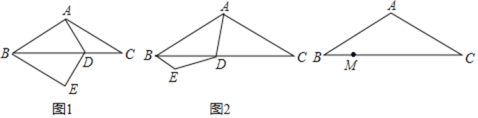
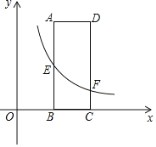
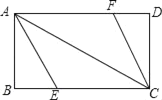
【题目】同学张丰用一张长18cm、宽12cm矩形纸片折出一个菱形,他沿矩形的对角线AC折出∠CAE=∠DAC,∠ACF=∠ACB的方法得到四边形AECF(如图).
(1)证明:四边形AECF是菱形;
(2)求菱形AECF的面积.
【答案】(1)详见解析;(2)156.
【解析】
(1)先证明四边形AECF是平行四边形,再证明AF=CE即可.
(2)在RT△ABE中利用勾股定理求出BE、AE,再根据S菱形AECF=S矩形ABCD﹣S△ABE﹣S△DFC求出面积即可.
(1)证明:∵四边形ABCD是菱形,
∴AD∥BC,
∴∠FAC=∠ACE,
∵∠CAE=∠DAC,∠ACF=∠ACB,
∴∠EAC=∠ACF,
∴AE∥CF,∵AF∥EC,
∴四边形AECF是平行四边形,
∵∠FAC=∠FCA,
∴AF=CF,
∴四边形AECF是菱形.
(2)解:∵四边形AECF是菱形,
∴AE=EC=CF=AF,设菱形的边长为a,
在RT△ABE中,∵∠B=90°,AB=12,AE=a,BE=18﹣a,
∴a2=122+(18﹣a)2,
∴a=13,
∴BE=DF=5,AF=EC=13,
∴S菱形AECF=S矩形ABCD﹣S△ABE﹣S△DFC=216﹣30﹣30=156cm2.


练习册系列答案
相关题目