题目内容
【题目】如图，在直角坐标系内，O为原点，点A的坐标为(10，0)，点B在第一象限内，BO＝5，sin∠BOA＝
. 求：(1)点B的坐标；(2)cos∠BAO的值．
【答案】（1）点B的坐标为(4，3)；（2）cos∠BAO＝
.
【解析】试题分析：（1）作BH⊥OA， 垂足为H，在Rt△OHB中，根据锐角三角函数的定义及已知条件求得BH的长，再根据勾股定理求得OH的长，即可得点B的坐标；（2）先求得AH的长，在Rt△AHB中，根据勾股定理求得AB的长，根据锐角三角函数的定义即可求得cos∠BAO的值．
试题解析：
(1)如图所示，作BH⊥OA， 垂足为H．
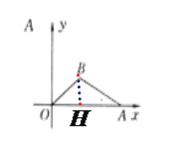
在Rt△OHB中，∵BO＝5，sin∠BOA＝
，∴BH=3，∴OH＝4，∴点B的坐标为(4，3)．
(2)∵OA＝10，OH＝4，∴AH＝6．在Rt△AHB中，∵BH=3，∴AB＝
，∴cos∠BAO=
= 
．
练习册系列答案
相关题目
【题目】某文具店准备购进A、B两种型号的书包共50个进行销售，两种书包的进价、售价如下表所示：
书包型号 | 进价（元/个） | 售价（元/个） |
A型 | 200 | 300 |
B型 | 100 | 150 |
购进这50个书包的总费用不超过7300元，且购进B型书包的个数不大于A型书包个数的
．
（1）该文具店有哪几种进货方案？
（2）若该文具店购进的50个书包全部售完，则该文具店采用哪种进货方案，才能获得最大利润？最大利润是多少？（利润＝售价﹣进价）
