题目内容
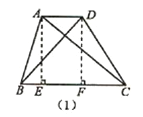
【题目】在平行四边形ABCD中,点O是对角线BD中点,点E在边BC上,EO的延长线与边AD交于点F,连接BF、DE,如图1.

(1)求证:四边形BEDF是平行四边形;
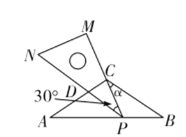
(2)在(1)中,若DE=DC,∠CBD=45°,过点C作DE的垂线,与DE、BD、BF分别交于点G、H、R,如图2.
①当CD=6,CE=4时,求BE的长.
②探究BH与AF的数量关系,并给予证明.
【答案】(1)详见解析;(2)①4![]() ﹣2;②AF=
﹣2;②AF=![]() BH,详见解析
BH,详见解析
【解析】
(1)由“ASA”可得△BOE≌△DOF,可得DF=BE,可得结论;
(2)①由等腰三角形的性质可得EN=CN=2,由勾股定理可求DN,由等腰三角形的性质可求BN的长,即可求解;
②如图,过点H作HM⊥BC于点M,由“AAS”可证△HMC≌△CND,可得HM=CN,由等腰直角三角形的性质可得BH=![]() HM,即可得结论.
HM,即可得结论.
(1)证明:∵平行四边形ABCD中,点O是对角线BD中点,
∴AD∥BC,BO=DO,
∴∠ADB=∠CBD,且∠DOF=∠BOE,BO=DO,
∴△BOE≌△DOF(ASA)
∴DF=BE,且DF∥BE,
∴四边形BEDF是平行四边形;
(2)①如图2,过点D作DN⊥EC于点N,

∵DE=DC=6,DN⊥EC,
∴EN=CN=2,
∴DN=![]() =
=![]() =4
=4![]() ,
,
∵∠DBC=45°,DN⊥BC,
∴∠DBC=∠BDN=45°,
∴DN=BN=4![]() ,
,
∴BE=BN﹣EN=4﹣2![]() ;
;
故答案为:BE=4﹣2![]() .
.
②AF=![]() BH,
BH,
理由如下:如图,过点H作HM⊥BC于点M,

∵DN⊥EC,CG⊥DE,
∴∠CEG+∠ECG=90°,∠DEN+∠EDN=90°,
∴∠EDN=∠ECG,
∵DE=DC,DN⊥EC,
∴∠EDN=∠CDN,EC=2CN,
∴∠ECG=∠CDN,
∵∠DHC=∠DBC+∠BCH=45°+∠BCH,∠CDB=∠BDN+∠CDN=45°+∠CDN,
∴∠CDB=∠DHC,
∴CD=CH,且∠HMC=∠DNC=90°,∠ECG=∠CDN,
∴△HMC≌△CND(AAS)
∴HM=CN,
∵HM⊥BC,∠DBC=45°,
∴∠BHM=∠DBC=45°,
∴BM=HM,
∴BH=![]() HM,
HM,
∵AD=BC,DF=BE,
∴AF=EC=2CN,
∴AF=2HM=![]() BH.
BH.
故答案为:AF=![]() BH.
BH.

 新思维寒假作业系列答案
新思维寒假作业系列答案