��Ŀ����
����Ŀ���ۺ���ʵ��
�Ķ����²��ϣ�
���壺���߷ֱ�����Ҽнǻ��������������ν��������������Ρ���
�÷������Ա�ʾΪ����ͼ�٣��ڡ�ABC���DEF�У����AC=DE����C+��E=180�㣬BC=EF����ô��ABC���DEF�ǻ��������Σ�
��֮���������ABC���DEF�ǻ��������Σ���ô��AC=DE����C+��E=180�㣬BC=EF��Ҳ�dz����ģ�
����̽��
����������ѧ֪ʶ�Լ�ȫ�������ε����֪ʶ������⣺
��1�����ʣ����������ε�������
��ͼ�ڣ���֪��ABC���DEF�ǻ��������Σ�
��֤����ABC���DEF�������ȣ�
֤�����ֱ�����ABC���DEF�ı�BC��EF�ϵĸ��ߣ����AGC=��DHE=90����
���� (��ʣ��֤�����̲�������)
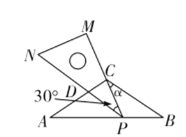
��2������������һ����ȫ�ȣ������жϸ�˵���Ƿ���ȷ����˵�����ɣ��������ȷ����ٳ�һ������������ʾ��ͼ��

���𰸡���1������������2������ȷ�����ɼ�����
��������
��1����֪��ABC����DEF�ǻ��������Σ��ɵá�ACB+��E=180����AC=DE��BC=EF��֤�á�ACG=��E��֤����AGC�ա�DHE���õ�AG=DH������![]() ������ABC����DEF�������ȣ�
������ABC����DEF�������ȣ�
��2������ȷ���Ȼ�������ͼ��֤����ABC�ա�DEF����ABC����DEF�ǻ��������Σ�����������һ����ȫ�ȵ�˵������
��1���ߡ�ABC����DEF�ǻ��������Σ�
���ACB+��E=180����AC=DE��BC=EF��
�֡ߡ�ACB+��ACG=180����
���ACG=��E��
����AGC����DHE��

���AGC�ա�DHE��AAS��
��AG=DH��
��![]()
����ABC����DEF�������ȣ�
��2������ȷ��
�������ͼ������ABC����DEF�У�

���ABC�ա�DEF��SAS����
���ABC����DEF�ǻ��������Σ�
���������һ����ȫ�ȵ�˵������


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�