题目内容
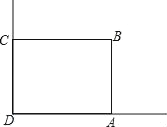
【题目】如图,某课外活动小组借助直角墙角(两边足够长)用篱笆围成矩形花园ABCD,篱笆只围AB、BC两边.已知篱笆长为40m,
(1)若篱笆围成的矩形ABCD的面积为300m2.求边AB的长.
(2)若篱笆围成的矩形面积S要最大,求边AB的长.
【答案】(1)10m或30m;(2)篱笆围成的矩形面积S最大时,边AB的长为20m.
【解析】
(1)直接利用长乘宽得出矩形面积进而得出答案;
(2)利用配方法求二次函数最值即可.
解:(1)设边AB的长为xm,则BC的长为(40﹣x)m,
依题意得:
x(40﹣x)=300
即x2﹣40x+300=0
∴x1=30,x2=10
∴AB的长为10m或30m;
(2)设边AB的长为xm,则BC的长为(40﹣x)m,
依题意得:
S=x(40﹣x)=﹣x2+40x=﹣(x﹣20)2+400,
当x=20时,S取最大值为400,
∴篱笆围成的矩形面积S最大时,边AB的长为20m.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目