题目内容
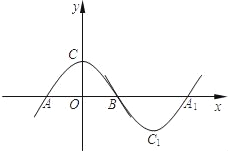
【题目】如图，抛物线m：y=ax2+b（a＜0，b＞0）与x轴于点A、B（点A在点B的左侧），与y轴交于点C．将抛物线m绕点B旋转180°，得到新的抛物线n，它的顶点为C1，与x轴的另一个交点为A1．若四边形AC1A1C为矩形，则a，b应满足的关系式为（ ）
A. ab=﹣2 B. ab=﹣3 C. ab=﹣4 D. ab=﹣5
【答案】B
【解析】分析：利用矩形性质得出要使平行四边形AC1A1C是矩形，必须满足AB=BC，即可求出．
详解：令x=0，得：y=b．∴C（0，b）．
令y=0，得：ax2+b=0，∴x=±
，∴A（﹣，0），B（，0），∴AB=2，BC=
=
．
要使平行四边形AC1A1C是矩形，必须满足AB=BC，∴2=．∴4×（﹣
）=b2﹣，∴ab=﹣3，∴a，b应满足关系式ab=﹣3．
故选B．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
