题目内容
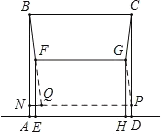
【题目】如图,正方形ABCD与矩形EFGH在直线![]() 的同侧,边AD,EH在直线
的同侧,边AD,EH在直线![]() 上,且AD=5 cm,EH=4 cm, EF=3 cm.保持正方形ABCD不动,将矩形EFGH沿直线
上,且AD=5 cm,EH=4 cm, EF=3 cm.保持正方形ABCD不动,将矩形EFGH沿直线![]() 左右移动,连接BF、CG,则BF+CG的最小值为( )
左右移动,连接BF、CG,则BF+CG的最小值为( )

A. 4B. ![]() C.
C. ![]() D. 5
D. 5
【答案】B
【解析】
作点C关于FG的对称点P,连接GP,以FG,PG为邻边作平行四边形PGFQ,则BF+CG=BF+QF,当B,F,Q三点共线时,BF+CG的最小值为BQ的长,过点Q作QN⊥AB于N,依据勾股定理即可得到在Rt△BNQ中,BQ=![]() ,即可得出BF+CG的最小值为
,即可得出BF+CG的最小值为![]() .
.
解:如图所示,作点C关于FG的对称点P,连接GP,
以FG,PG为邻边作平行四边形PGFQ,则FQ=PG=CG,FG=QP=4,
∴BF+CG=BF+QF,
∴当B,F,Q三点共线时,BF+CG的最小值为BQ的长,
过点Q作QN⊥AB于N,
由题可得BN=2(53)=4,NQ=54=1,
∴Rt△BNQ中,BQ=![]() ,
,
∴BF+CG的最小值为![]() ,
,
故选B.

练习册系列答案
相关题目
【题目】为了更好改善河流的水质,治污公司决定购买10台污水处理设备![]() 现有A,B两种型号的设备,其中每台的价格,月处理污水量如下表:经调查:购买一台A型设备比购买一台B型设备多2万元,购买2台A型设备比购买3台B型设备少6万元.
现有A,B两种型号的设备,其中每台的价格,月处理污水量如下表:经调查:购买一台A型设备比购买一台B型设备多2万元,购买2台A型设备比购买3台B型设备少6万元.
A型 | B型 | |
价格 | a | b |
处理污水量 | 240 | 200 |
![]() 求a,b的值;
求a,b的值;
![]() 治污公司经预算购买污水处理设备的资金不超过105万元,你认为该公司有哪几种购买方案;
治污公司经预算购买污水处理设备的资金不超过105万元,你认为该公司有哪几种购买方案;
![]() 在
在![]() 的条件下,若每月要求处理污水量不低于2040吨,为了节约资金,请你为治污公司设计一种最省钱的购买方案.
的条件下,若每月要求处理污水量不低于2040吨,为了节约资金,请你为治污公司设计一种最省钱的购买方案.