题目内容
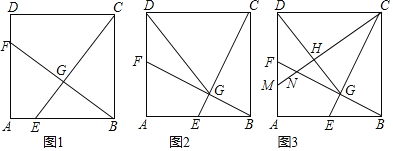
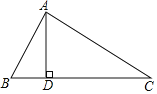
【题目】如图,在△ABC中,∠BAC=90°,AD⊥BC,垂足为D.
(1)求作∠ABC的平分线,分别交AD,AC于P,Q两点;(要求:尺规作图,保留作图痕迹,不写作法)
(2)在(1)的基础上,过点P画PE∥AC交BC边于E,联结EQ,则四边形APEQ是什么特殊四边形?证明你的结论.
【答案】(1)见解析;(2)四边形APEQ是菱形.理由见解析.
【解析】
(1)利用尺规作出∠ABC的角平分线即可.
(2)利用全等三角形的性质证明PA=PE,再证明AP=AQ,即可解决问题.
解:(1)如图,射线BQ即为所求.
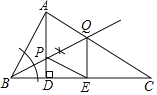
(2)结论:四边形APEQ是菱形.
理由:∵AD⊥BC,
∴∠ADB=90°,
∵∠BAC=90°,
∴∠ABD+∠BAD=90°,∠ABD+∠C=90°,
∴∠BAD=∠C,
∵PE∥AC,
∴∠PEB=∠C,
∠BAP=∠BEP,
∵BP=BP,∠ABP=∠EBP,
∴△ABP≌△EBP(AAS),
∴PA=PE,
∵∠AQP=∠QBC+∠C,∠APQ=∠ABP+∠BAP,
∴∠APQ=∠AQP,
∴AP=AQ,
∴PE=AQ,
∵PE∥AQ,
∴四边形APEQ是平行四边形,
∵AP=AQ,
∴四边形APEQ是菱形.

 名校课堂系列答案
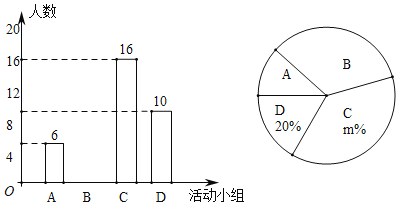
名校课堂系列答案【题目】九年级(1)班全班50名同学组成五个不同的兴趣爱好小组,每人都参加且只能参加一个小组,统计(不完全)人数如下表:
编号 | 一 | 二 | 三 | 四 | 五 |
人数 |
| 15 | 20 | 10 |
|
已知前面两个小组的人数之比是![]() .
.
解答下列问题:
(1)![]() .
.
(2)补全条形统计图:
(3)若从第一组和第五组中任选两名同学,求这两名同学是同一组的概率.(用树状图或列表把所有可能都列出来)

【题目】襄阳市某农谷生态园响应国家发展有机农业政策,大力种植有机蔬菜.某超市看好甲、乙两种有机蔬菜的市场价值,经调查,这两种蔬菜的进价和售价如下表所示:
有机蔬菜种类 | 进价(元/ | 售价(元/ |
甲 |
| 16 |
乙 |
| 18 |
(1)该超市购进甲种蔬菜10![]() 和乙种蔬菜5
和乙种蔬菜5![]() 需要170元;购进甲种蔬菜6
需要170元;购进甲种蔬菜6![]() 和乙种蔬菜10
和乙种蔬菜10![]() 需要200元.求
需要200元.求![]() ,
,![]() 的值;
的值;
(2)该超市决定每天购进甲、乙两种蔬菜共100![]() 进行销售,其中甲种蔬菜的数量不少于20
进行销售,其中甲种蔬菜的数量不少于20![]() ,且不大于70
,且不大于70![]() .实际销售时,由于多种因素的影响,甲种蔬菜超过60
.实际销售时,由于多种因素的影响,甲种蔬菜超过60![]() 的部分,当天需要打5折才能售完,乙种蔬菜能按售价卖完.求超市当天售完这两种蔬菜获得的利润额
的部分,当天需要打5折才能售完,乙种蔬菜能按售价卖完.求超市当天售完这两种蔬菜获得的利润额![]() (元)与购进甲种蔬菜的数量
(元)与购进甲种蔬菜的数量![]() (
(![]() )之间的函数关系式,并写出
)之间的函数关系式,并写出![]() 的取值范围;
的取值范围;
(3)在(2)的条件下,超市在获得的利润额![]() (元)取得最大值时,决定售出的甲种蔬菜每千克捐出
(元)取得最大值时,决定售出的甲种蔬菜每千克捐出![]() 元,乙种蔬菜每千克捐出
元,乙种蔬菜每千克捐出![]() 元给当地福利院,若要保证捐款后的盈利率不低于20%,求
元给当地福利院,若要保证捐款后的盈利率不低于20%,求![]() 的最大值.
的最大值.