Question

【题目】如图，图中小方格都是边长为1的正方形，△ABC与△A′B′C′是关于点G为位似中心的位似图形，它们的顶点都在小正方形顶点上．

（1）画出位似中心点G；

（2）若点A、B在平面直角坐标系中的坐标分别为（﹣6，0），（-3，2），点P（m，n）是线段AC上任意一点，则点P在△A′B′C′上的对应点P′的坐标为　　．

Answer 1

【答案】（1）作图见解析；（2）P′的坐标为（2m,2n）

【解析】试题分析：（1）连接C′C并延长交A′A的延长线于点G；（2）在线段AC上随机取一点P，连接OP并延长与线段A′C′的交点即为P′，作P′E⊥x轴，PF⊥x轴，不难证明△POF∽△P′OE，由此可得==，然后充分利用位似三角形的性质，求出，即可求出、，即可求出P′E、OE的长度，点P′的坐标即可表示出来.

试题解析：

(1)

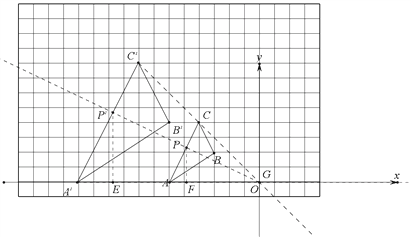
（2）如图建立直角坐标系，在线段AC上随机取一点P，连接OP并延长与线段A′C′的交点即为P′，作P′E⊥x轴，PF⊥x轴，

∵P′E⊥x轴，PF⊥x轴，

∴∠P′EO=∠PFO=90°，

∵∠POF=∠P′OE，

∴△POF∽△P′OE，

∴==，

∵OA=6，O A′=12，

∴=，

∵△OAP与△OA′P′是关于点G为位似中心的位似图形，

∴==，

∴==，

∵PF=n，OF=－m，

∴P′E=2n，OE=－2m，

∴P′（2m，2n）.