题目内容
【题目】已知⊙O的直径为10,点A、点B、点C在⊙O上,∠CAB的平分线交⊙O于点D.


(1)如图①,若BC为⊙O的直径,AB=6,求AC,BD的长;
(2)如图②,若∠CAB=60°,CF⊥BD,①求证:CF是⊙O的切线;②求由弦CD、CB以及弧DB围成图形的面积.
【答案】⑴AC=8,BD=5![]() ;⑵①证明见解析;②
;⑵①证明见解析;②![]() .
.
【解析】试题分析:(1)要求AC的长,将AC放在Rt△ABC中,利用勾股定理可求得;要求BD的长,先证明△BCD为等腰直角三角形,再结合勾股定理可求出;(2)①连接OC,证明∠OCF=90°即可;②通过证明△CGD≌△OGB,可以得到S△CGD=S△OGB,由此将阴影部分面积转化为扇形DOB的面积,利用扇形面积公式求出即可.
试题解析:
(1)∵BC为⊙O的直径,
∴∠CAB=∠CDB=90°,
∵BC=10,AB=6,
∴AC=![]() =8,
=8,
∵AD平分∠CAB,
∴∠CAD=∠DAB=45°,
∴CD=BD,
∵CD2+BD2=BC2,
∴2BD2=100,
∴BD=5![]() ;
;
(2)
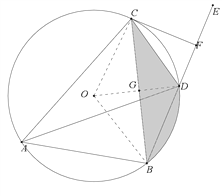
连接CO、OD、OB,
∵∠CAB=60°,AD平分∠CAB,
∴∠CDB=120°,∠COB=120°,∠CAD=∠DAB=30°,
∴∠CDF=60°, ![]() =
=![]() ,
,
∴∠COD=∠BOD=60°,
∵OC=OD,
∴∠OCD=60°,
∵CF⊥BD,
∴∠CFD=90°,
∴∠DCF=30°,
∴∠OCF=90°,
∴CF是⊙O的切线;
∵OC=OB,∠COD=∠BOD,
∴OG⊥BC,
∵∠OCD=60°,∠COD=60°,
∴△COD为等边三角形,
∴OG=GD,∠CDG=∠DOB=60°,
在△CGD和△OGB中,
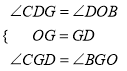 ,
,
∴△CGD≌△OGB,
∴S△CGD=S△OGB,
∴S阴影=S扇形BOD=![]() =
=![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目