题目内容
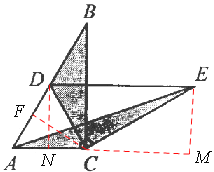
【题目】如图1,将两个完全相同的三角形纸片ABC和DEC重合放置,其中∠C=900,∠B=∠E=300.



(1)操作发现如图2,固定△ABC,使△DEC绕点C旋转。当点D恰好落在BC边上时,填空:线段DE与AC的位置关系是 ;
② 设△BDC的面积为S1,△AEC的面积为S2。则S1与S2的数量关系是 。
(2)猜想论证
当△DEC绕点C旋转到图3所示的位置时,小明猜想(1)中S1与S2的数量关系仍然成立,并尝试分别作出了△BDC和△AEC中BC,CE边上的高,请你证明小明的猜想。
(3)拓展探究
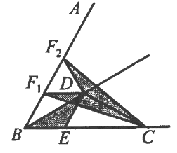
已知∠ABC=600,点D是其角平分线上一点,BD=CD=4,OE∥AB交BC于点E(如图4),若在射线BA上存在点F,使S△DCF =S△BDC,请直接写出相应的BF的长
【答案】解:(1)①DE∥AC。②![]() 。
。
(2)![]() 仍然成立,证明如下:
仍然成立,证明如下:
∵∠DCE=∠ACB=900,∴∠DCM+∠ACE=1800。
又∵∠ACN+∠ACE=1800,∴∠ACN =∠DCM 。
又∵∠CAN=CMD==900,AC=CD,∴△ANC≌△DMC(AAS)。∴AN=DM。
又∵CE=CB,∴![]() 。
。
(3) ![]() 或
或![]() 。
。
【解析】(1)①由旋转可知:AC=DC,
∵∠C=900,∠B=∠DCE=300,∴∠DAC=∠CDE=600。∴△ADC是等边三角形。
∴∠DCA=600。∴∠DCA=∠CDE=600。∴DE∥AC。
②过D作DN⊥AC交AC于点N,过E作EM⊥AC交AC延长线于M,过C作CF⊥AB交AB于点F。
由①可知:△ADC是等边三角形, DE∥AC,∴DN=CF,DN=EM。
∴CF=EM。
∵∠C=900,∠B =300,∴AB=2AC。
又∵AD=AC,∴BD=AC。
∵![]() ,∴
,∴![]() 。
。
(2)通过AAS证明△ANC≌△DMC,即可得AN=DM,从而由CE=CB得到![]() 。
。
(3)如图所示,作DF1∥BC交BA于点F1,作DF2⊥BD交BA于点F2。F1,F2即为所求。
按照(1)(2)求解的方法可以计算出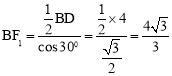 ,
,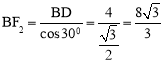 。
。

 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案






