题目内容
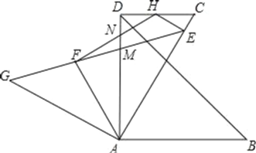
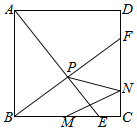
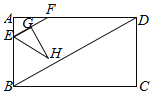
【题目】如图,矩形ABCD中,AB=6,∠ABD=60°,点E从点A出发,以每秒2个单位长度的速度沿边AB运动,到点B停止运动.过点E作EF∥BD交AD于点F,将△AEF绕点E顺时针旋转得到△GEH,且点G落在线段EF上,设点E的运动时间为t(秒)(0<t<3).
(1)若t=1,求△GEH的面积;
(2)若点G在∠ABD的平分线上,求BE的长;
(3)设△GEH与△ABD重叠部分的面积为T,用含t的式子表示T,并直接写出当0<t<3时T的取值范围.
【答案】(1)2![]() ;(2)3;(3)T=
;(2)3;(3)T=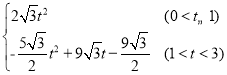 .
.
【解析】
(1)根据四边形ABCD是矩形和EF∥BD,可推出AE和AF的长,即可求出答案;
(2)由BG平分∠ABD,可得∠EBG=![]() ∠ABD=30°,再根据∠AEG=∠EBG+∠EGB=60°,可得∠EBG=∠EGB=30°,即可推出BE的长;
∠ABD=30°,再根据∠AEG=∠EBG+∠EGB=60°,可得∠EBG=∠EGB=30°,即可推出BE的长;
(3)当点H落在BD上时,作EJ⊥BD于J,根据EF∥BD,推出△EBH是等边三角形,从而得出t=1,再分当0<t≤1时和当1<t<3时两种情况讨论即可.
解:(1)如图1中,
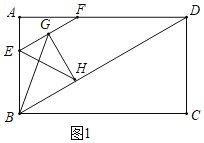
∵四边形ABCD是矩形,
∴∠A=90°,
∵EF∥BD,
∴∠AEF=60°,
∵AE=2,
∴AF=AEtan60°=![]() ,
,
∴S△EGH=S△AEF=![]() AEAF=
AEAF=![]() ×2×
×2×![]() =
=![]() ;
;
(2)如图2中,
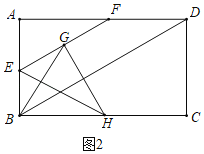
由题意得,BG平分∠ABD,
∴∠EBG=![]() ∠ABD=30°,
∠ABD=30°,
∵∠AEG=∠EBG+∠EGB=60°,
∴∠EBG=∠EGB=30°,
∴BE=EG=AE=3;
(3)如图1﹣1中,当点H落在BD上时,作EJ⊥BD于J,
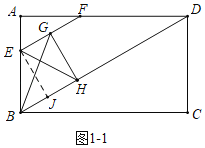
∵EF∥BD,
∴∠FEH=∠EHB=60°,
∴△EBH是等边三角形,
∴EH=EB=EF=2AE,
∴AE=2,BE=4,
∴t=1,
如图3中,当0<t≤1时,重叠部分是△EGH,T=S△AEF=![]() ×2t×2t×
×2t×2t×![]() =
=![]() t2,
t2,
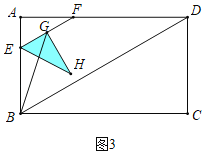
如图4中,当1<t<3时,重叠部分是四边形MNGE,作EJ⊥BD于J,
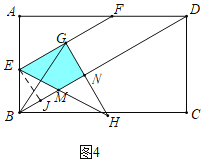
在Rt△EBJ中,∵BE=6﹣2t,∠EBJ=60°,
∴BJ=![]() BE=3﹣t,EJ=
BE=3﹣t,EJ=![]() BJ=3
BJ=3![]() ﹣
﹣![]() t,
t,
∵△EBM是等边三角形,
∴BJ=JM=3﹣t,
∵四边形EGNJ是矩形,
∴EG=NJ=2t,
∴MN=NJ﹣MJ=3t﹣3,
∴T=![]() (MN+EG)EJ=
(MN+EG)EJ=![]() (3t﹣3+2t)(3
(3t﹣3+2t)(3![]() ﹣
﹣![]() t)=
t)=![]() t2+9
t2+9![]() t
t![]() ,
,
综上所述,T=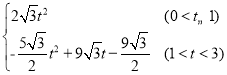 .
.